
中学三年間の集大成!
”中3数学”の学習ポイント

今までの数学はいかがでしたか?
いよいよ残すところはあと中3の範囲です!
これまでに学習した2年分の知識を使うので、難易度もグググっと上がってきますよ!
もし中3の授業を受けていて、
「前にやった気がするけど覚えていない…」
「なんとなく全体的にわからない…」
そんなお子さんは、1・2年生のところであやふやな部分があるかもしれません。
今すぐ中1数学や中2数学をチェックしてみて下さい!
中3数学ではこんなことを学習します。
すごい量ですね。
でもひとつひとつ確実に理解していけば大丈夫!
このページでは中3の数学で押さえておきたい「多項式の計算」「因数分解」「平方根」「二次方程式」の基礎ポイントをご紹介させていただきます。
こんなページも見られています!
>>中学3年生の教科別学習ポイント

2021年4月から中学校の教科書が全面的に改訂され、新しい学習指導要領による授業が開始されました。「数学」は、全ての学年に「データの活用」が追加され、これまで以上にグラフや資料から必要なことを”読み取る力”が重視されています。
もっと詳しく知りたい!
>>2021年からの中学数学はデータだらけ!?

式の計算がパワーアップ!
多項式の計算
計算がニガテな子には少し苦しくなってくるのがこの“多項式の計算”です。
中2の初めに習った“式の計算”の応用でもあるので、もし忘れてしまっている方は中2数学の「式の計算」を見返してしっかり復習しましょう!
★多項式の計算★
① 多項式と単項式の乗法・除法
多項式と単項式の乗法
まずは多項式と単項式どうしをかけるやり方からやっていきます!
\((2a+b)×2a\)
<手順1>
単項式を( )の中の多項式の項に1つずつかける。
\((2a+b)×2a\)
\(=2a\textcolor{red}{×2a}+b\textcolor{red}{×2a}\)
<手順2>
同類項をまとめる
\((2a+b)×2a\)
\(=2a×2a+b×2a\)
\(=4a^2+2ab\)
多項式と単項式の除法
次に、多項式と単項式どうしを割る場合の計算を見ていきましょう!
\((8a^2-12a)÷2a\)
<手順1>
単項式を( )の中の多項式の項に1つずつ割る。
\((8a^2-12a)÷2a\)
\(=8a^2\textcolor{red}{÷2a}-12a\textcolor{red}{÷2a}\)
<手順2>
同類項をまとめる
\((8a^2-12a)÷2a\)
\(=8a^2÷2a-12a÷2a\)
\(=4a-6\)
★多項式の計算★
② カッコどうしの展開
ここから新しい計算方法が出てきます。
後々習う”因数分解”の基本にもなっていくので、取りこぼしのないようにしていきましょう。
カッコどうしの展開というのは、例えばこのような計算です。
今まで見たことがない形ですね。
ここで大切なのは”計算する順序”です。ゆっくりやればカンタンですよ!
\((x+2)(x+3)\)
<手順①>
左の \(x\) と右の \(x\) をかけます。
\(x×x=\textcolor{red}{x^2}\)
<手順②>
左の \(+2\) と右の \(+3\) を足した数に \(x\) をかけます。
\((2+3)×x=\textcolor{red}{+5x}\)
<手順③>
左の \(+2\) と右の \(+3\) をかけます。
\(2×3=\textcolor{red}{+6}\)
<手順④>
①②③を並べたのが答えです。
\(\textcolor{red}{x^2+5x+6}\)
\((x+2)(x+3)\)
\(=\textcolor{red}{x^2+5x+6}\)
★多項式の計算★
③ 乗法公式
乗法の公式は大きく分けて4種類。
これらの公式を覚えて理解することが絶対的に必要です!
乗法公式(超重要!)
公式①
\(\textcolor{red}{(x+a)(x+b)=x^2+(a+b)x+ab}\)
公式②
\(\textcolor{red}{(a+b)^2=a^2+2ab+b^2}\)
公式③
\(\textcolor{red}{(a-b)^2=a^2-2ab+b^2}\)
公式④
\(\textcolor{red}{(a+b)(a-b)=a^2-b^2}\)
公式②③は「平方の公式」
公式④は「和と差の積」とも言います。
これらの公式はとても重要なものなので、何度も書いたり、何度もぶつぶつ言ったりして確実に覚えてください!
そして、定期テストや入試テストで出てきたら、感覚的に使いこなせるようにしましょう!
実際どんな感じの問題が出るのか練習してみましょう!
\(\textcolor{red}{(x+a)(x+b)}\)の展開
【問題】次の式を展開しなさい
\((x+4)(x+6)\)
公式①を使います。
\(\textcolor{red}{(x+a)(x+b)=x^2+(a+b)x+ab}\)
\(x^2+(4+6)x+(4×6)\)
\(=x^2+10x+24\)
\(\textcolor{red}{(a+b)^2}\)の展開
【問題】次の式を展開しなさい
\((x+6)^2\)
公式②を使います。
\(\textcolor{red}{(a+b)^2=a^2+2ab+b^2}\)
\(x^2+(2×x×6)+6^2\)
\(=x^2+12x+36\)
\(\textcolor{red}{(a-b)^2}\)の展開
【問題】次の式を展開しなさい
\((x-4)^2\)
公式③を使います。
\(\textcolor{red}{(a-b)^2=a^2-2ab+b^2}\)
\(x^2+(2×x×-4)+(-4)^2\)
\(=x^2-8x+16\)
\(\textcolor{red}{(a+b)(a-b)}\)の展開
【問題】次の式を展開しなさい
\((x+5)(x-5)\)
公式④を使います。
\(\textcolor{red}{(a+b)(a-b)=a^2-b^2}\)
\(x^2-5^2\)
\(=x^2-25\)
カッコカッコの展開計算は、手順通りやれば点数が取りやすいですよ。
公式も確実に覚えて使えるようにしてもらいたいですが、もし公式を忘れてしまっても、②カッコどうしの展開のやり方でも解けるので、何度も練習してくださいね!
数学の大きな壁に突入!
因数分解
3年生になってぶつかる大きな壁が”因数分解”です。
これは2年生で習った”式の計算”の派生になるのですが、”因数分解”は一味も二味もちがいます!
高校入試にもよく出ますし、大きく差が付く分野なので、しっかりやり方を掴んでください!
★因数分解★
① 因数と素数
因数とは…?
多項式を積の形にしたときのそれぞれの項を”因数”って言います。
例えば・・・
\(14\) は \(7×2\) と表されるので「\(7\)」と「\(2\)」は \(14\) の因数となります。
他にはこんなのもあります。
例えば、\((x+2)(x+5)\) を展開すると \(x^2+7x+10\) になります。
そしてこの \(x^2+7x+10\) を“積の形”にすると
\(x^2+7x+10=(x+2)(x+5)\) となります。
この右辺にある、\((x+2)\) と \((x+5)\) のことを \(x^2+7x+10\) の“因数”と言います。
素数とは…?
\(2\)、\(3\)、\(5\)、\(7\)…のような“これ以上小さい自然数の積の形で表すことのできない”自然数を“素数”と言います。
ただし1は素数には含めません。
例えばこんなのが素数
「\(19\)」…自然数の積の形での表し方は「\(1×19\)」しかありません。
しかしこれだと「\(19\)」よりも小さくはありませんね。
ですので「\(19\)」は素数です。
「\(31\)」…これも「\(1×31\)」以外で表すことはできません。
ですので「\(31\)」も素数です。
これは素数ではありません。
「\(27\)」…自然数の積の形で表すと「\(1×27\)」もありますが「\(9×3\)」のように「\(27\)」より小さい自然数の積で表すことができました。
ですのでこれは素数ではありません。
「\(56\)」…これも同じように自然数の積で表してみると「\(8×7\)」「\(28×2\)」「\(14×4\)」など、「\(56\)」より小さい自然数の積の形で表すことができます。
ですのでこれは素数ではありません。
素数や因数はこの後の因数分解を理解する上でめちゃめちゃ大事になってくるので、絶対マスターしよう!
★因数分解★
② 素因数分解
素因数分解とは…?
自然数を素数(ただし1以外)の積として表すことを素因数分解と言います。
では例として \(150\) を素因数分解してみます。
\(150\) は「\(15×10\)」と表せますね。
その次に「\(15\)」と「\(10\)」はそれぞれ「\(5×3\)」と「\(5×2\)」で表せます。
これ以上分解できなくなりましたね。
ですので \(150\) を素因数分解すると…
\(150=5×3×5×2=2×3×5^2\)
となり、この \(2\)、\(3\)、\(5^2\) を”素因数”といいます。
他にもいくつかやってみましょう
\(45\) を素因数分解しなさい
\(45=9×\textcolor{red}{5}\)
\(9=3×3=\textcolor{red}{3^2}\)
\(45=3^2×5\)
答え. \(3^2×5\)
\(160\) を素因数分解しなさい
\(160=16×10\)
\(16=4×4\)
\(4=\textcolor{red}{2×2}\)、\(4=\textcolor{red}{2×2}\)
\(10=\textcolor{red}{2×5}\)
\(\textcolor{red}{2×2×2×2×2×5}=2^5×5\)
答え. \(2^5×5\)
素因数分解も「習うより慣れろ」です!
たくさん練習してくださいね!
★因数分解★
③ 因数分解のやり方
多項式を「単項式×単項式」「多項式×多項式」の形にすることを因数分解と言います。
これだけだとイメージが湧かないと思うので実際にやってみましょう!
\(x^2+7x+10\) を因数分解するとどうなるでしょうか?
ここでさきほどの“乗法公式”を思い出してみましょう。
この公式に当てはめて考えてみると、
たして「\(+7\)」になり、かけて「\(+10\)」になる2つの数を探せばいいということになりますね。
まず、かけて「\(+10\)」になる2数を考えます。
「\(+1\)と\(+10\)」「\(+5\)と\(+2\)」「\(-1\)と\(-10\)」「\(-5\)と\(-2\)」の4パターンが、かけて「\(+10\)」になります。
次に、足して「\(+7\)」になる2数を考えます。
「\(+7\)と\(0\)」「\(+6\)と\(+1\)」「\(+5\)と\(+2\)」「\(+4\)と\(+3\)」ですね。
※他にもたくさんありますが…
ということは、たして「\(+7\)」になり、かけて「\(+10\)」になる2つの数は「\(\textcolor{red}{+5}\)と\(\textcolor{red}{+2}\)」であることがわかりました。
\(=(x+5)(x+2)\)
となり、
答えは \(\textcolor{red}{(x+5)(x+2)}\) となります。
これで因数分解は完了です!
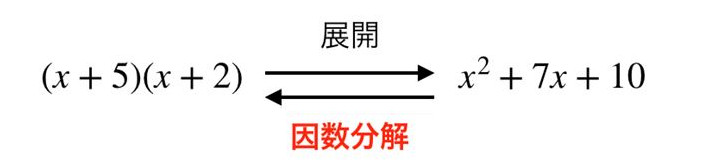
因数分解は「元に戻す」というイメージです。
今回の \(x^2+7x+10\) を元に戻してあげると \((x+5)(x+2)\) といった具合です。
いくつかやってみましょう!
次の式を因数分解しなさい。
① \(x^2+9x+14\)
足して \(+9\)、かけて \(+14\) になる2数を探します。
\(+2\) と \(+7\) ですね。
答え. \(\textcolor{red}{(x+2)(x+7)}\)
② \(x^2-x-30\)
足して \(-1\)、かけて \(-30\) になる2数を探します。
\(+5\) と \(-6\) ですね。
答え. \(\textcolor{red}{(x+5)(x-6)}\)
③ \(x^2-10x+24\)
足して \(-10\)、かけて \(+24\) になる2数を探します。
\(-4\) と \(-6\) ですね。
答え. \(\textcolor{red}{(x-4)(x-6)}\)
④ \(x^2+10x+25\)
足して \(+10\)、かけて \(+25\) になる2数を探します。
\(+5\) と \(+5\) ですね。
この場合は、\((x+5)(x+5)\) と書かずに、\((x+5)^2\) と書きます。
答え. \(\textcolor{red}{(x+5)^2}\)
因数分解は中3の定期テストや本番の入試テスト(特に大問1)に必ず出ます!
何度も解いて練習して絶対マスターしましょう!
★因数分解★
④ 公式の利用
因数分解は問題によって解き方が異なる場合があります。
いろいろな問題パターンに対応できるように、公式を使って因数分解をするやり方もあります。
先ほどの”乗法公式”をもう一度見てみましょう!
公式①
\(\textcolor{red}{(x+a)(x+b)=x^2+(a+b)x+ab}\)
公式②
\(\textcolor{red}{(a+b)^2=a^2+2ab+b^2}\)
公式③
\(\textcolor{red}{(a-b)^2=a^2-2ab+b^2}\)
公式④
\(\textcolor{red}{(a+b)(a-b)=a^2-b^2}\)
この中で、公式④はやり方をしっかり掴まないと対応出来なくなりますのでいくつか練習してみましょう。
【問題】
\(x^2-16\) を因数分解しなさい。
\(x^2-16\) の \(16\) は \(4^2\) と表すことができます。
ということは、\(x^2-4^2\) となります。
ここで公式④の \(\textcolor{red}{(a+b)(a-b)=a^2-b^2}\) にあてはめると、
\(x^2-4^2=(x+4)(x-4)\) になりますね。
答え. \(\textcolor{red}{(x+4)(x-4)}\)
【問題】
\(x^2-100\) を因数分解しなさい。
\(x^2-100\) の \(100\) は \(10^2\) と表すことができます。
ということは、\(x^2-10^2\) となります。
ここで公式④の \(\textcolor{red}{(a+b)(a-b)=a^2-b^2}\) にあてはめると、
\(x^2-10^2=(x+10)(x-10)\) になりますね。
答え. \(\textcolor{red}{(x+10)(x-10)}\)
【問題】
\(x^2-81\) を因数分解しなさい。
\(x^2-81\) の \(81\) は \(9^2\) と表すことができます。
ということは、\(x^2-9^2\) となります。
ここで公式④の \(\textcolor{red}{(a+b)(a-b)=a^2-b^2}\) にあてはめると、
\(x^2-9^2=(x+9)(x-9)\) になりますね。
答え. \(\textcolor{red}{(x+9)(x-9)}\)
★因数分解★
⑤ 共通因数の取り出し
共通因数を使うやり方
\(Ma+Mb\) のように多項式の中の共通の因数を取り出すやり方もあります。
その際に使う公式がこちら!
そもそも「共通因数」ってどういうことかというと、
例えば…、
「\(2x^2+2x\)」だと、「\(2x^2\)」と「\(2x\)」でどちらも「\(2x\)」が含まれていることがわかります。
これを共通因数と言います。
つまり、「\(2x^2+2x\)」 の共通因数は「\(2x\)」となります!
これを式にすると、
\(2x^2+2x=2x×x+2x×1\)
そしてこの「\(2x\)」を取り出してあげると、
\(2x(x+1)\)となります。
=\(2x(x+1)\)
では他にもやってみましょう!
【問題】
次の式から共通因数を取り出し、因数分解しなさい。
\(6x^2+2x\)
まずはじめに「\(6x^2\)」と「\(2x\)」の共通因数を探してみましょう。
「\(6x^2\)」…\(2x×3x\)
「\(2x\)」…\(2x×1\)
このように表すと、共通因数が「\(2x\)」だということがわかりました。
これを式にすると、
\(6x^2+2x\)
\(=2x×3x+2x×1\)
最後にこの共通因数「\(2x\)」を取り出してあげると…
\(=2x×3x+2x×1\)
\(=2x(3x+1)\)
答え. \(2x(3x+1)\)
中3の因数分解では、他にもたくさんの問題パターンがあります。
マニアックなくらい難しい問題もありますが、基本の形は絶対に抑えておいてくださいね。
ルートを理解しよう
平方根
中1の方程式は中3では二次方程式に、中2の一次関数は中3では二次関数に。
この「平方根」は中3になって初めて聞く単元です。
そんな平方根ですが、実は中1で習った範囲に密接に関わっているのです!
★平方根★
① 平方根とは…?
中学1年生のときに「\(2^2=4\)」や「\(4^2=16\)」のような”累乗”というものを習いましたね。
平方根を学習していく上で、累乗の知識がかなり重要になってきます。
それも踏まえてみていきましょう。
平方根とは…?
2乗すると \(a\) になる数を「 \(a\) の平方根」と言います。
つまり \(a\) の平方根は、\(x^2=a\) を成立させる \(x\) の値のことです。
これだけだとよくわかりませんよね。
まずは一旦例を見てみましょう!
【例題①】
\(25\) の平方根はなんでしょう?
□\(^2=25\) とすると、□にはどんな数字が入るでしょうか。
まず \(5\) が入りそうですね。\(5^2\) は \(25\) になります。
しかし、実はあともう一つあります。 それは \(-5\) です。
\((-5)^2\) は同じく \(25\) になります。
これらを踏まえると
\(25\) の平方根は \(±5\) となります。
では次の例題はどうでしょうか?
【例題②】
\(5\) の平方根はなんでしょう?
さっきの例題①と同じように□\(^2=5\) と考えてみると、□にはどんな数が入りそうでしょうか?
なんだか入らなそうですよね。
こんな時に出てくるのが、そう!
\(√\) です!
この記号の名前は「根号」と言います。
読み方は「ルート」と読みます。
例えば \(\sqrt{7}\) だったら読み方は「ルート7」です。
そして \(√\) の性質として知っておいて欲しいことがあります。
それは、
「 \(\sqrt{a}×\sqrt{a}\) 」でルートが外れて「 \(a\) 」になる!
ということです!
これを用いることで \(5\) の平方根を表すことができます。
先ほどの□\(^2=5\) の□を \(x\) に置き換えて \(x^2=5\) として説明していきます。
改めて、どんな数字を2乗したら \(x^2=5\) が成り立つのかというと、
「 \(\sqrt{a}×\sqrt{a}\) 」でルートが外れて「 \(a\) 」になる!
の性質から「 \(\sqrt{5}×\sqrt{5}\) 」で「 \(5\) 」になることがわかります。
同じように「 \((-\sqrt{5})×(-\sqrt{5})\) 」も「 \(5\) 」になることがわかります。
つまりこれらを踏まえると、\(x=±\sqrt{5}\) となり、
「 \(5\) 」の平方根は \(±\sqrt{5}\) だということがわかります。
★平方根★
② ルートの中を簡単に!
<パターン1>
ルートをなくす。
ルートの中の2乗の因数を探そう!
ルートの中を簡単にするというのは、ルートの中身を外に出して整数にするということです。
例えば \(\sqrt{9}\) の場合、中身の「 \(9\) 」を素因数分解すると「 \(3×3\) 」、つまり「 \(3^2\) 」になりますね。
ルートの中身に2乗の因数がある場合は、ルートをなくして整数にすることができます。
ルートの外に出すときは”2乗を取る”ということも忘れないで下さい!
\(\sqrt{16}\) もやってみましょう。
ルートの中身「 \(16\) 」は「 \(4×4\) 」、つまり \(4^2\) になります。
ということは、
では、\(\sqrt{6}\) はどうでしょう?
ルートの中身「 \(6\) 」を素因数分解すると「 \(2×3\) 」になります。
2乗の因数がありませんね。
ということは、\(\sqrt{6}\) は簡単にすることは出来ません。
ルートの中の数字に2乗の因数がある場合はルートを外して簡単にすることができるのです!
ではいくつかやってみましょう!
次の平方根を簡単にしなさい。
(1)\(\sqrt{81}\)
(2)\(\sqrt{36}\)
(3)\(\sqrt{100}\)
答え.
(1)\(\sqrt{81}=\sqrt{9^2}=\textcolor{red}{9}\)
(2)\(\sqrt{36}=\sqrt{6^2}=\textcolor{red}{6}\)
(3)\(\sqrt{100}=\sqrt{10^2}=\textcolor{red}{10}\)
<パターン2>
ルートの外に出す。
\(\sqrt{18}\) を簡単にしてみましょう。
先ほどと同じように、ルートの中身「 \(18\) 」を素因数分解します。
ルートの中に「 \(3^2\) 」がありますね。
ルート内に2乗の因数がある場合はルートの外に出すことができましたよね。
\(\sqrt{75}\) もやってみましょう!
まずルート内の「 \(75\) 」を素因数分解します。
ルートの中に「 \(5^2\) 」がありますね。
では「 \(5^2\) 」を外に出して簡単にします。
他にもいくつかやってみましょう!
【問題】次の平方根を簡単にしなさい
(1)\(\sqrt{32}\)
(2)\(\sqrt{96}\)
(3)\(\sqrt{180}\)
答え.
(1)\(\sqrt{32}\)
\(=\sqrt{2×2×2×2×2}\)
\(=\sqrt{2^4×2}\)
\(=\sqrt{4^2×2}\)(← \(2^4\) を \(4^2\) に変えます)
\(=\textcolor{red}{4\sqrt{2}}\)
(2)\(\sqrt{96}\)
\(=\sqrt{2×2×2×2×2×3}\)
\(=\sqrt{2^4×6}\)
\(=\sqrt{4^2×6}\)(← \(2^4\) を \(4^2\) に変えます)
\(=\textcolor{red}{4\sqrt{6}}\)
(3)\(\sqrt{180}\)
\(=\sqrt{2×2×3×3×5}\)
\(=\sqrt{2^2×3^2×5}\)
\(=2×3\sqrt{5}\)
\(=\textcolor{red}{6\sqrt{5}}\)
例えば、\(\sqrt{18}\) と \(3\sqrt{2}\) は同じ大きさの数ですが、定期テストでは「平方根は簡単にして書きなさい」という指示をされることが多いです。
その場合は、\(\sqrt{18}\) と書いてしまうとバツになります…。
平方根を簡単にする方法は絶対にマスターしてください。
あまり大きくない数字の場合は、因数分解をしなくても頭の中で計算できるように何度も練習していきましょう!
★平方根★
③ 分母の有理化
これから平方根の計算を学習していく中で、分数の計算もたくさん出てきます。
分母にルートがある分数では、分母にルートを含まない形に変える必要があります。
この分母にルートを含まないかたちに変えることを「分母の有理化」といいます。
では \(\frac{1}{\sqrt{5}}\) を有理化してみましょう。
分母の \(\sqrt{5}\) に注目。
\(\sqrt{5}\) に \(\sqrt{5}\) をかければルートが外れて \(5\) になりますよね。
これを利用して、分母と分子にそれぞれ \(\sqrt{5}\) をかけます。
これで分母にルートが含まれない形になりました。
\(\frac{1}{\sqrt{5}}\) を有理化して、\(\frac{\sqrt{5}}{5}\) となりました。
では \(\frac{2}{\sqrt{3}}\) も有理化してみましょう。
分母に \(\sqrt{3}\) があるので、分母と分子に \(\sqrt{3}\) をかけます。
\(\frac{2}{\sqrt{3}}\) を有理化して、\(\frac{2\sqrt{3}}{3}\) となりました。
\(\frac{3}{\sqrt{18}}\) はどうでしょう?
「 \(\sqrt{18}\) を分母・分子にかければいいんでしょ!」
ちょっと待ってください!
この場合はもう1つやらなければならない手順があるんです!
先ほど説明した「ルートの中を簡単にする」を思い出してください。
\(\sqrt{18}\) って簡単に出来そうですよね!
\(18\) を素因数分解すると、\(3^2×2\) となるので「2乗の因数」があります。
その場合はルートの外に出すことが出来ましたよね。
このように、ルートの中を簡単にしてから分母の有理化をしていきます。
これから出てくる平方根の計算問題では、常にルートの中を簡単に出来るかを意識してください。
簡単に出来る場合は簡単にしてから計算するようにしていきましょう。
では \(\frac{3}{\sqrt{18}}\) の有理化に戻ります。
ますは分母の \(\sqrt{18}\) を \(3\sqrt{2}\) にします。
\(\frac{3}{3\sqrt{2}}\) を有理化します。
分母にある \(\sqrt{2}\) を分母・分子にそれぞれかけます。
\(\frac{3}{3\sqrt{2}}\) \(=\) \(\frac{3\textcolor{red}{×\sqrt{2}}}{3\sqrt{2}\textcolor{red}{×\sqrt{2}}}\)\(=\) \(\frac{3\sqrt{2}}{3×2}\) \(=\) \(\frac{3\sqrt{2}}{6}\)
最後に約分して…\(\frac{\sqrt{2}}{2}\)
これで \(\frac{3}{\sqrt{18}}\) を有理化したら\(\textcolor{red}{\frac{\sqrt{2}}{2}}\) になりました。
いくつか練習してみましょう。
次の数の分母を有理化しなさい。
(1)\(\frac{4}{\sqrt{6}}\) (2)\(\frac{\sqrt{5}}{3\sqrt{7}}\) (3)\(\frac{3\sqrt{2}}{2\sqrt{32}}\)
答え.
(1)\(\frac{4}{\sqrt{6}}\)
\(=\) \(\frac{4×\sqrt{6}}{\sqrt{6}×\sqrt{6}}\) \(=\) \(\frac{4\sqrt{6}}{6}\) \(=\) \(\textcolor{red}{\frac{2\sqrt{6}}{3}}\)
(2)\(\frac{5}{3\sqrt{7}}\)
\(=\) \(\frac{\sqrt{5}×\sqrt{7}}{3\sqrt{7}×\sqrt{7}}\) \(=\) \(\frac{\sqrt{35}}{3×7}\) \(=\) \(\textcolor{red}{\frac{\sqrt{35}}{21}}\)
(3)\(\frac{3\sqrt{2}}{2\sqrt{32}}\)
\(=\) \(\frac{3\sqrt{2}}{2×4\sqrt{2}}\) (← \(\sqrt{32}\) を \(4\sqrt{2}\) にします)
\(=\) \(\frac{3\sqrt{2}×\sqrt{2}}{8\sqrt{2}×\sqrt{2}}\)
\(=\) \(\frac{3×2}{8×2}\) \(=\) \(\textcolor{red}{\frac{3}{8}}\)
分母の有理化が出来ないと、平方根の分数が含まれる計算がまったく出来なくなってしまいます。
何度も練習してしっかり自分のモノにしてください!
★平方根★
④ 平方根の乗法・除法
ここから根号を含む「かけ算・わり算」をやっていきます!
今までの基本が出来ていればカンタンですよ!
\(\sqrt{2}×\sqrt{3}\) をやってみます。
ルートどうしのかけ算はルートの中身をかけるだけ!
メッチャ簡単ですね!
ではこの場合はどうでしょう?
ルートの外どうしと中どうしをかけるだけ!
これもカンタン!!
\(=\) \(\textcolor{red}{8\sqrt{6}}\)
わり算(除法)もおんなじ考え方でOK!
ルートの外どうし、中どうしを割るだけ!
\(=8÷2×\sqrt{6÷3}\)
\(=\textcolor{red}{4\sqrt{2}}\)
ルートの中が簡単に出来る場合は簡単にしてから計算したほうが楽ですよ!
例えばこういうヤツ。
いきなりルートの中の \(32\) と \(27\) をかけて \(\sqrt{864}\) としてから因数分解して簡単にしてもいいのですが、これだと計算がメッチャ大変…。
先にルート内を簡単にしてから計算しましょう。
\(=4\sqrt{2}×3\sqrt{3}\)
\(=\textcolor{red}{12\sqrt{6}}\)
★平方根★
⑤ 平方根の加法・減法
ここから根号を含む「たし算・ひき算」です。
先ほどやった「かけ算・わり算」よりも格段と難しくなりますので、1歩1歩確実に理解していきましょう!
まず大前提を覚えてください。
ルート内が同じ数字だけ!
↑これ!とっても大事!
先ほどのかけ算・わり算の場合と大きく違うところはココになります!
例えばこの式。
ルートの中が \(2\) と \(3\) でちがう数字ですね
ということは、これ以上計算ができないということになります。
この式も…
これもルートの中が \(2\) と \(5\) でちがう数字ですので計算できません。
ではこれはどうでしょう?
ルートの中の数字が同じ \(2\) ですね!
では計算してみましょう。
ルートの外を計算して、ルートの中はそのままにします。
※ルート内は絶対に足したり引いたりしてはいけません。
\(=(3+4)\sqrt{2}\)
\(=\textcolor{red}{7\sqrt{2}}\)
これは中1で習った文字式と同じ考え方です。
\(3\textcolor{red}{x}+4\textcolor{red}{x}=7\textcolor{red}{x}\) ですね。
文字の部分( \(\textcolor{red}{x}\) )が同じなので数字の部分(係数)を足すことができました。
\(3\textcolor{red}{x}+4\textcolor{blue}{y}\) の場合はどうでしょうか?
文字の部分が \(\textcolor{red}{x}\) と \(\textcolor{blue}{y}\) で異なるので、計算は出来ませんでしたよね。
根号(ルート)が含まれる計算も、文字式と同じ考え方なのです。
よくあるミス
これらは全部バツです!
\(\sqrt{3}+\sqrt{3}=\sqrt{6}\)
(正解は\(2\sqrt{3}\))
\(2\sqrt{5}+4\sqrt{5}=6\sqrt{10}\)
(正解は\(6\sqrt{5}\))
\(2\sqrt{3}+3\sqrt{5}=5\sqrt{8}\)
(これ以上計算できない)
\(8\sqrt{5}-5\sqrt{3}=3\sqrt{2}\)
(これ以上計算できない)
ルート内の数字は足したり引いたりは出来ません!
間違いやすいので気を付けてください。
いくつかやってみましょう。
次の式を簡単にしなさい。
(1)\(5\sqrt{3}−2\sqrt{3}\)
(2)\(−4\sqrt{5}−3\sqrt{5}\)
(3)\(2\sqrt{2}+3\sqrt{3}−5\sqrt{2}\)
答え.
(1)\(5\sqrt{3}−2\sqrt{3}=\textcolor{red}{3\sqrt{3}}\)
(2)\(−4\sqrt{5}−3\sqrt{5}=\textcolor{red}{−7\sqrt{5}}\)
(3)\(2\sqrt{2}+3\sqrt{3}−5\sqrt{2}\)
\(=2\sqrt{2}−5\sqrt{2}+3\sqrt{3}\)(順序を変えた)
\(=\textcolor{red}{−3\sqrt{2}+3\sqrt{3}}\)(これ以上計算できない)
何度も言いますが…
ルートの中が同じ数字どうしなら、足したり引いたりすることができます。
ルートの中が違う数字どうしの場合は、足したり引いたりすることはできません。
ただし!!
それはルート内の数字を簡単にした後の話です!
ではこの場合はどうでしょうか?
ルートの中の数字が違いますね。
でもこの場合は計算が出来るのです!
\(\sqrt{18}\) を簡単にすると \(\textcolor{red}{3\sqrt{2}}\) に!
\(\sqrt{32}\) を簡単にすると \(\textcolor{red}{4\sqrt{2}}\) に!
つまり・・・
\(\sqrt{18}+\sqrt{32}\) は、
\(\textcolor{red}{3\sqrt{2}+4\sqrt{2}}\) になるのです。
これならルートの中の数字が同じ「 \(2\) 」なので計算が出来ますよね!
一見ルート内が違う数字どうしでも、このように計算できることもあるので、まずはルートを簡単に出来るかどうかを一番先に考えるようにしてください!
最後にこいつに挑戦です!
分数がありますね…
しかも分母にルートがあるので、まずは \(\frac{\sqrt{3}}{\sqrt{2}}\) を有理化します。
分母が \(\sqrt{2}\) なので、分母と分子それぞれに \(\sqrt{2}\) をかけます。
これで \(\frac{\sqrt{3}}{\sqrt{2}}\) が \(\textcolor{red}{\frac{\sqrt{6}}{2}}\) になりました。
次に \(\sqrt{24}\) を簡単にします。
\(\sqrt{24}\) は \(\textcolor{red}{2\sqrt{6}}\) になりますね。
\(\frac{\sqrt{3}}{\sqrt{2}}\) \(-\sqrt{24}\) が \(\textcolor{red}{\frac{\sqrt{6}}{2}}\) \(\textcolor{red}{-2\sqrt{6}}\) になりました。
ルートの中が同じ数字「 \(6\) 」になったので計算が出来ますね。
分数があるので分母を同じ数字(通分)にして計算します。
\(\frac{\sqrt{6}}{2}\) \(-2\sqrt{6}=\)\(\frac{\sqrt{6}}{2}\) \(-\) \(\frac{4\sqrt{6}}{2}\) \(=\textcolor{red}{-}\)\(\textcolor{red}{\frac{3\sqrt{6}}{2}}\)
\(\frac{\sqrt{3}}{\sqrt{2}}\) \(-\sqrt{24}\) の答えは… \(\textcolor{red}{-}\)\(\textcolor{red}{\frac{3\sqrt{6}}{2}}\)
平方根の加法(たし算)・減法(ひき算)は文字式の考え方と同じです。
文字式は \(x\) とか \(y\) とかの文字でしたが、平方根は文字ではなく \(\sqrt{2}\) や \(\sqrt{3}\) というように数字が入っているので紛らわしく感じてしまいますよね。
ルートどうしの加法・減法は、ルートの中の数字は足したり引いたりはできないので、ルート内の数字は \(x\) とか \(y\) のような文字であると考えたほうがいいですよ!
方程式がパワーアップ!
二次方程式
中1の前半で「方程式」というものを習いましたが、中3になると「二次方程式」となって再登場します!
二次方程式は、中1の方程式はもちろん、これまでに習った「因数分解」「平方根」などの理解も必要になりますので、あやふやなお子さんはしっかり復習しながら進めてくださいね!
1年生で習った「方程式」はこんなのでした。
\(-2x=-5x+9\)
\(-3(x-1)=2x-3\)
このように、\(x\)(他の文字でもOK)を求める式でしたよね。
二次方程式とは…?
例えばこんなの。
\(x^2+7x+10=0\)
\(2x^2-6x-3=0\)
このように「 \(x\) などの未知の数値の2乗まで含んでいる方程式」を二次方程式といいます。
二次方程式には3つの解き方があります。
② 因数分解を使って解く
③ 解の公式を使って解く
式の形によって解きやすい方法が変わりますので、この3つの方法は絶対にマスターしてください。
「平方根がわからない」「因数分解がわからない」という子は、このページで説明した平方根、因数分解に戻ってもう一度理解を深めましょう!
★二次方程式★
① 平方根を使って解く
平方根を使って解く方法は、二次方程式の中でも比較的シンプルな形が多いです。
例えばこんなの
平方根で習った形にしてみると、
\(x=±\sqrt{16}\)
\(\textcolor{red}{x=±4}\)
※解に\(±\)がつくことを忘れないで下さい。
これはどうでしょう?
これも同じやり方でいけます!
\(x=±\sqrt{8}\)
\(\textcolor{red}{x=±2\sqrt{2}}\)
こんなやつもOK!
\(2x^2=24\)
\(x^2=12\)
\(x=±\sqrt{12}\)
\(\textcolor{red}{x=±2\sqrt{3}}\)
変形だけどこんなのもOK!
2乗の展開をしないでカッコをつけたままの計算でいきます!
\((x-4)^2=9\)
\((x-4)=±\sqrt{9}\)
\(x-4=±3\)
\(x-4=3\) より、\(x=7\)
\(x-4=-3\) より、\(x=-1\)
こんな形の二次方程式では、平方根を使った解き方で求めていきましょう!
\((x+a)^2=\) 〇〇
★二次方程式★
② 因数分解を使って解く
平方根を使ったやり方では解けない形の2次方程式では、因数分解を使って解いていきます。
例えばこれは因数分解後の形ですが、
左の \(x\) に \(-1\) を代入すると左辺が \(0\) になります。
右の \(x\) に \(3\) を代入すると左辺が \(0\) になります。
右辺が \(0\) なので、答えは、\(x=-1\) 、\(3\) となります。
このように因数分解をして \((x+a)(x+b)=0\) の形にして、\(a\) と \(b\) の符号を変えた形が二次方程式の解となるのです。
いくつかやってみましょう。
(1)\(x^2-3x+2=0\)
(2)\(x^2+5x-6=0\)
(3)\(x^2+6x+8=0\)
答え.(1)
\(x^2-3x+2=0\)
\((x-1)(x-2)=0\)
\(x=1、2\)
答え.(2)
\(x^2+5x-6=0\)
\((x-1)(x+6)=0\)
\(x=1、-6\)
答え.(3)
\(x^2+6x+8=0\)
\((x+2)(x+4)=0\)
\(x=−2、−4\)
ちょっと応用。
少しひねった問題もやってみましょう。
(1)\((x+5)^2=0\)
(2)\((x+2)(x+4)=-1\)
(3)\(-x^2-10x-25=0\)
答え.(1)
\((x+5)^2=0\)
この形は、\((x+5)(x+5)=0\) と同じですね。
ということは、\(x=-5\) になります。
このように \((x+a)^2=0\) の形では、解が1つになるので覚えておいてください。
\(x=-5\)
答え.(2)
\((x+2)(x+4)=-1\)
よく見ると右辺が \(-1\) になっていますね。こういう場合は右辺が \(0\) の形に変えていきます。
まずは左辺を展開します。
\((x+2)(x+4)=-1\)
\(x^2+6x+8=-1\) (左辺を展開)
\(x^2+6x+8+1=0\)
\(x^2+6x+9=0\)
\((x+3)^2=0\)
\(x=-3\)
答え.(3)
\(-x^2-10x-25=0\)
先頭の \(x^2\) にマイナスがついていますね。
この場合は両辺に \(-1\) をかけて、\(-x^2\) を \(x^2\) にします。
\(-x^2-10x-25=0\)
\(-1×(-x^2-10x-25)=-1×0\)
(両辺に-1をかける)
\(x^2+10x+25=0\)
\((x+5)^2=0\)
答え.\(x=-5\)
★二次方程式★
③ 解の公式を使って解く
これまで①平方根を使う解き方と②因数分解を使う解き方をやってきました。
ところが、平方根も使えない、因数分解も使えない形の二次方程式が出てきます。
例えばこんなの!
この式、左辺の部分を因数分解できるでしょうか??
\(x^2-7x+1\) を因数分解すると…
かけて \(+1\)、たして -7 の2数って???
どんなに計算が得意な子でも、この2数を頭の中で計算して出すことは絶対に出来ません!
そこで便利なのが、
解の公式!
この公式!絶対に暗記してください!
\(ax^2+bx+c=0\) の解は、
\(x=\) \(\frac{-b±\sqrt{b^2-4ac}}{2a}\)
これ、超超超大切な公式です!
定期テストや入試テストにも二次方程式の解の公式の問題は必ずでます。
何度も声に出して、何度もノートに書いて、トイレにも貼って、暗記です!!
では先ほどの二次方程式を、解の公式を使って解いてみます。
\(ax^2+bx+c=0\)
↑この式より、
\(x^2-7x+1=0\) は、
\(a=1、b=−7、c=1\) ですね。
では解の公式の \(a,b,c\) にそれぞれを代入して計算してみましょう!
\(x=\) \(\frac{-b±\sqrt{b^2-4ac}}{2a}\)
↑\(a=1、b=−7、c=1\) を代入する。
\(x=\) \(\frac{-\textcolor{red}{(-7)}±\sqrt{\textcolor{red}{(-7)}^2-4\textcolor{red}{×1×1}}}{2\textcolor{red}{×1}}\)
\(x=\) \(\frac{7±\sqrt{45}}{2}\)
\(x=\) \(\frac{7±3\sqrt{5}}{2}\)(←これが答え!)
こいつもやってみます!
\(ax^2+bx+c=0\)
↑この式より、
\(2x^2-4x-5=0\) は、
\(a=2、b=−4、c=-5\) ですね。
では解の公式の \(a,b,c\) にそれぞれを代入して計算してみましょう!
\(x=\) \(\frac{-b±\sqrt{b^2-4ac}}{2a}\)
↑\(a=2、b=−4、c=-5\) を代入する。
\(x=\) \(\frac{-\textcolor{red}{(-4)}±\sqrt{\textcolor{red}{(-4)}^2-4\textcolor{red}{×2×(-5)}}}{2\textcolor{red}{×2}}\)
\(x=\) \(\frac{4±\sqrt{56}}{4}\)
\(x=\) \(\frac{4±2\sqrt{14}}{4}\)
\(x=\) \(\frac{2±\sqrt{14}}{2}\)(←これが答え!)
いかがでしたか?
ここで紹介した二次方程式の計算は、全て基本的な形のみです。
さらに難しい問題もたくさん出てきますが、1つ1つ手順通りに計算していけば大丈夫!
二次方程式は、式の形によって解き方が異なります。
②因数分解を使って解く
③解の公式を使って解く
こんな形なら平方根!
\(x^2=16\)、\((x+3)^2=25\) など。
こんな形で因数分解できるなら因数分解!
\(x^2+2x+1=0\)、\(x^2-6x+9=0\) など。
平方根も因数分解もできないなら解の公式!
\(x^2+8x+4=0\)、\(2x^2-6x-3=0\) など。
それぞれの解き方を何度も練習して自分のモノにしてください!

このページでは、中学3年生の数学で押さえておきたい重要ポイントである“多項式の計算”、“因数分解”、“平方根”、“二次方程式”について説明させていただきました。
この後に習う、”二次関数”や“相似図形”、”三平方の定理”なんかも超大事です!
冒頭でもお伝えしましたが、数学は思いっきり積み重ねの教科です。
基本があやふやなままだと、あっという間にわからなくなってしまう恐ろしい教科です。
そこに対抗していくには、“基礎の土台”が超重要!
基礎を完璧に理解していけば、あとは練習を重ねることによってどんどん数学が面白くなっていきますよ!
「因数分解がわからない…」
「二次方程式なんて大っキライ!」
そんなお子さんは今すぐ対策をしていかないと、高校受験の数学が大変になってしまいます。

私たち家庭教師のジャニアスでは、“数学の楽しさ”を教えてたくさんのお子さんに成績アップ、志望校合格の結果を出してきました。
今なら!無料の体験授業で勉強のやり方から丁寧に教えていますので、この機会に一度試してみませんか?
もちろん、体験授業を受けていただいたからといって、ご入会への無理な勧誘は一切ありませんのでご安心ください。
体験授業でお会いできることをスタッフ一同、楽しみにしています。

今ご覧になっているページは
数学(中3)です。
▼ よく見られているページ ▼

家庭教師のジャニアスでは下記の地域にお住いの方に家庭教師を紹介しております。下記に含まれていない地域にお住まいのご家庭でも、家庭教師を紹介できる場合もございますので、お気軽にお問い合わせください。

私たちジャニアスは、どんなに効果がある勉強法でもお子さんに合わない・
続けることができなければ「意味がない」と考えています。

塾や家庭教師選びにご苦労されているご家庭も多いと思いますが、ジャニアスの体験授業は、「やる気のきっかけにしたい」「今の塾と比べてみたい」「今すぐは考えてないけど家庭教師がどんなモノかを見てみたい」などのような、気軽な気持ちで受けていただけたらと思います。
もちろん、体験を受けたからといって、無理に入会を勧めるようなことは一切ありませんので、安心してくださいね(^^)











































