
中学数学はデータまみれ!?
教科書改訂でどう変わった?
「中学校の数学ってどう変わるの?」
「教科書が改正されたって聞いたけど…」
「高校の内容が移行されたってホント?」
2021年度の教科書改訂に基づいて、中学校の数学が大きく変わったことをご存知ですか?
新しい学習指導要領に基づく学校教育が小学校で2020年の3月から始まり、次いで中学校が2021年度(令和3年度)、高等学校が2022年度(令和4年度)に全面的に始まります。
ただでさえ「算数」から「数学」に変わり、一気に難しくなると言われている中で、2021年度からいよいよ中学校の数学も本格的に新学習指導要領が導入されました。
改訂後の数学の教科書を見てみると、全ての学年の最後に「データの活用」というものが追加されています。
「データ」って、今までは理科の実験結果とかで使われることがほとんどでしたが、それが数学でも出てくるのです。なんだか難しそうですよね…。
「うちの子がついていけるのかしら…」
「データの解析なんて、超ムズそう…」
このページでは、小学校高学年や中学生のお子さんをお持ちのご家庭に向けて、新しい中学校数学がどのように変わり、どのように対応していくべきかを、実際の具体例と共にご紹介していきます。
>>中学校の教科書改訂【5教科】を見る
~中学数学はここが大きく変わる!~
新たに追加された”データの活用”
新しい学習指導要領では「データ分析」を重要視しています。それに伴って今回の改訂で、中学数学の教科書に新しく加わったのは次の3つ。
- 累積度数
- 反例
- 四分位範囲と箱ひげ図
それぞれが「データの活用」による分析や問題解決などに役立つ分野となっています。
こちらは数学の教科書の目次です。
2020年までと2021年からの新旧の比較を表にしたので、とくに追加された項目をチェックしてみてください。
| 中1数学の新旧比較 | |||
|---|---|---|---|
| 2020年まで | 2021年から | ||
| 1章 | 正の数・負の数 | 1章 | 正の数・負の数 ・素数 ・素因数分解 |
| 2章 | 文字の式 | 2章 | 文字の式 |
| 3章 | 方程式 | 3章 | 方程式 |
| 4章 | 変化と対応 | 4章 | 変化と対応 |
| 5章 | 平面図形 | 5章 | 平面図形 |
| 6章 | 空間図形 | 6章 | 空間図形 |
| 7章 | 資料の活用 | 7章 | データの活用 ・度数分布表 ・累積度数 |
中1数学は1章の正の数・負の数に素数と素因数分解が追加。7章にデータの活用(度数分布表・累積度数)が追加。
| 中2数学の新旧比較 | |||
|---|---|---|---|
| 2020年まで | 2021年から | ||
| 1章 | 式の計算 | 1章 | 式の計算 |
| 2章 | 連立方程式 | 2章 | 連立方程式 |
| 3章 | 一次関数 | 3章 | 一次関数 |
| 4章 | 図形の調べ方 | 4章 | 図形の調べ方 |
| 5章 | 図形の性質と証明 | 5章 | 図形の性質と証明 ・反例 |
| 6章 | 確率 | 6章 | 場合の数と確率 |
| 7章 | 箱ひげ図とデータの活用 | ||
中2数学は5章の図形の性質と証明に反例が追加。7章に箱ひげ図とデータの活用が追加。
| 中3数学の新旧比較 | |||
|---|---|---|---|
| 2020年まで | 2021年から | ||
| 1章 | 式の展開と因数分解 | 1章 | 式の展開と因数分解 |
| 2章 | 平方根 | 2章 | 平方根 ・真の値と近似値 |
| 3章 | 二次方程式 | 3章 | 二次方程式 |
| 4章 | 関数 𝑦=𝑎𝑥² | 4章 | 関数 𝑦=𝑎𝑥² |
| 5章 | 図形と相似 | 5章 | 図形と相似 |
| 6章 | 円の性質 | 6章 | 円の性質 |
| 7章 | 三平方の定理 | 7章 | 三平方の定理 |
| 8章 | 標本調査 | 8章 | 標本調査とデータの活用 |
中3数学は2章の平方根に真の値と近似値が追加。8章の標本調査にデータの活用が追加。
どの学年にも最後の章あたりに「データの活用」がありますね。
なぜ、今回の教科書改訂で中学数学に「データの活用」を重視した変更を行ったのでしょうか?
少し掘り下げて解説していきます。
~大改定後の中学数学~
データを活用する論理的思考
私たちの身の回りにはたくさんの情報が溢れています。私たち現代人が1日に受け取る情報量は、江戸時代の1年分とも言われているほどです。
ですが、そのような“ビッグデータ”を正しく分析して結論を出し、その結論をもとに改善案を提案できる人材が圧倒的に不足していると言われています。
このことから、文部科学省は今回の大改訂で、中学数学の授業に「データの活用」を重視した変更を行ったのです。
改訂前の中1の教科書には、最後の章にほんの少し触れる程度に「資料の作成」という項目がありましたが、それが「データの活用」という項目に変更されました。
中2にも中3にも、最後の章に「データの活用」があるように、これからの中学数学は、計算問題や文章問題、図形問題ができればいいというわけではなくなりました。
これからの中学数学では、今までの学習項目に加えて、統計やグラフなど複雑なデータの情報を整理してシンプルにしていく授業が行われていきます。
データの情報を活用して整理していく上で必要な論理的思考は、将来、社会人になったときの基本的スキルとしても重要になっていきます。
データを活用する論理的思考の育成が、社会への適応能力や、私たちを取り巻く問題の解決にも繫がっていくのですね。
今回の改訂で新しく追加されたこの項目…
- 累積度数
- 反例
- 四分位範囲と箱ひげ図
これらは「データの活用」を重視したからこその追加になっているというわけですね。
~中学数学はここが大きく変わる!~
中1に移行・追加された4項目
2021年からの中学校数学の改訂で、最も大きく変化したのは中学1年生と言えるでしょう。
他の学年からの移行や、新たに追加された項目は次の4項目です。
- 素数(小5から移行)
- 素因数分解(中3から移行)
- 累積度数(新しく追加)
- 度数分布と確率(中2から移行)
では、それぞれを詳しく見ていきましょう。
~中1数学に移行・追加された項目~
素数
今までは小学5年生で学習していた「素数」を、中学1年生で学習するようになりました。新中1生は復習って感じにもなりますね。
ここで少しだけ「素数」を解説していきます。
素数とは…?
1より大きな整数(自然数)で、1またはその数だけが割り切れる数。簡単に言うと、2つしか約数がない数のことです。
約数とは…?
ある数(整数)を割り切ることのできる数(整数)です。
例えば、
「6」の約数は何でしょう?
割り切れる数が約数ですので、
6を割り切ることができる整数は、1、2、3、6なので、6の約数は、1、2、3、6です。割り切れるというのは、余りが0(余りが出ない)ということも確認してください。
では質問を変えます。
「6」は素数でしょうか?
素数というのは、1とその数だけが割り切れる数で、1を含めた2つしか約数がない数でした。
6の約数は、1、2、3、6と4つの約数があるので、「6」は素数ではありません。
では、
「3」は素数でしょうか?
まずは、3の約数を調べます。
3を割り切れる数、つまり約数は1と3だけです。
ですので、「3」は素数であると言えます。
このように素数であるかを判断していきます。
実際に定期テストでは…、
「次の数で素数を全て選びなさい」
「1~30までの整数のうち素数を全て書きなさい」
「1~50までの数のうち素数は全部で何個ですか」
こんな感じで出題されます。
~中1数学に移行・追加された項目~
素因数分解
今まで中学3年生で習っていた「素因数分解」が、中学1年生で学習するようになりました。
ここでは少しだけ素因数分解を解説していきます。
素因数分解とは…?
自然数を素数の積で表すこと。つまり、自然数を素数だけのかけ算で表してあげることを素因数分解といいます。
では、自然数100を素因数分解してみましょう。
素因数分解は「素数だけのかけ算」ですので、こうなります。
5×5は、52にします。
2×2も、22にします。
つまり、100を素因数分解したら「52×22」になるというわけです。
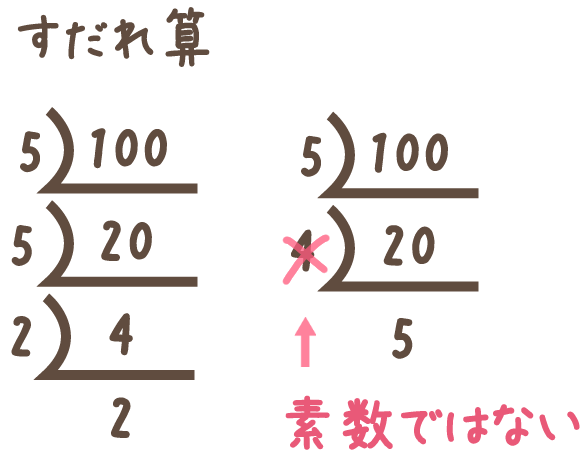
ちなみに4は素数ではないので(約数が1、2、4と3つあるので)、左側に置くことはできません。
やり方がつかめたら、カンタンに素因数分解が出来ちゃいますよね!
素因数分解と因数分解
ちなみに中3になると「因数分解」を習います。
因数分解はここでお話しした「素因数分解」とは考え方が全く違うので気を付けてください。
名前が似ているのでややこしいですが、因数分解は素因数分解よりも難しく、同じ意味で捉えてしまうと大変ですので…。
~中1数学に移行・追加された項目~
累積度数
「データの活用」という項目の中で、累積度数、度数分布、確率を学習していきます。
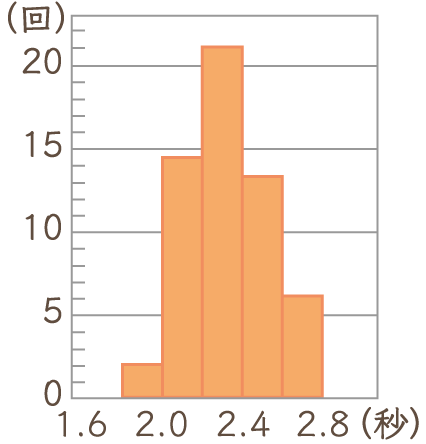
ヒストグラムも出来てきます。
右のようなグラフで、柱状グラフ(ちゅうじょうグラフ)ともいいます。
階級の幅を横、度数を縦とするグラフです。
今回の改訂で新しく追加された「累積度数(るいせきどすう)」は、データの活用の項目の中で、中学1年生の授業ででます。
累積度数とは…?
最初の階級から、ある階級までの度数の合計のこと。
つまり、度数を次々に足した数のことです。
難しいですよね…
階級って?度数って?
頭に「?」が出来ちゃいましたよね…。
度数分布表を見ながら解説していきます。
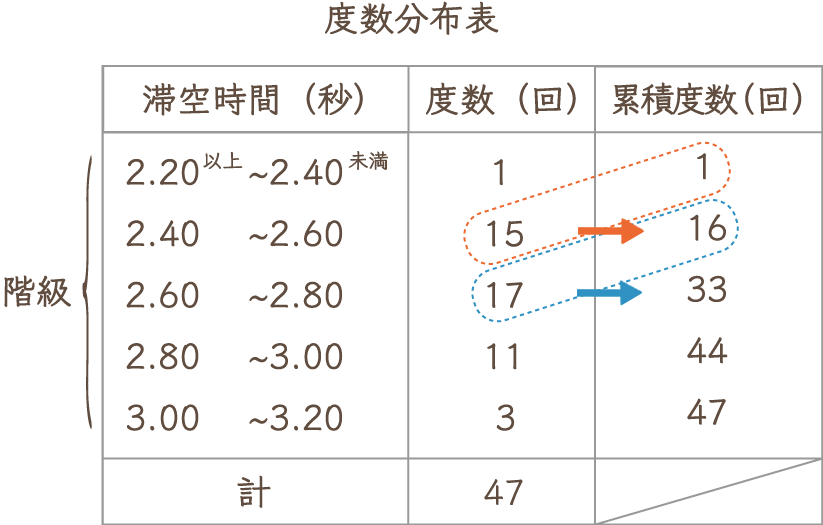
上の表にあるひとつひとつの区間を「階級」と言います。それぞれの階級に入るデータの個数を、その階級の「度数」っていいます。この階級ごとに整理された表を「度数分布表」といいます。
この表によって、データがどこら辺に集中しているのかがひと目でわかります。例えば、定期テストの点数なんかも「クラスの中でどのくらいの点数が多いか」などがわかるのです。
~中1数学に移行・追加された項目~
度数分布と確率
今までは中2で学習していた「確率」を、中1で学習することになりました。
確率とは…?
何かをしたときに○○の結果が起きる割合のこと。
中1で学習する「確率」は「観察や試行によって得られる確率」となっていて、中2で習う計算中心の学習とは異なり、データの読み取りがメインとなります。
このときの確率を求めるために必要なのが「相対度数」です。
相対度数とは…?
各階級の度数が全体の中でどれだけの割合にあたるかを示す値とのこと。
相対度数は、階級の度数と度数の合計を使って求められます。
下の表は、500円玉と100円玉をそれぞれ何回も投げて、オモテとウラの出た回数をまとめたものです。この表から、500円玉と100円玉ではどちらの方が、オモテが出やすいと言えるでしょうか?
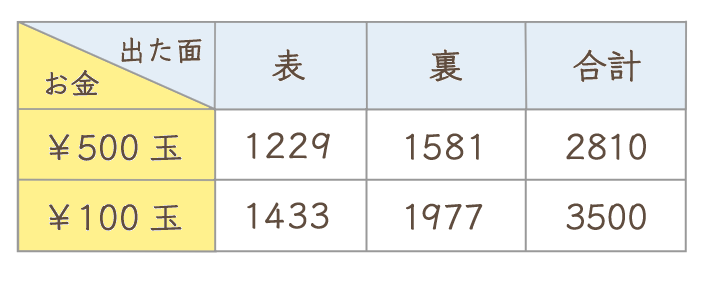
それぞれの相対度数を求めてみます。
<500円玉のオモテが出た相対度数>
1229÷2810=約0.437
<100円玉のオモテが出た相対度数>
1433÷3500=約0.409
500円玉のオモテが出た相対度数は、約0.437
100円玉のオモテが出た相対度数は、約0.409
これを見ると、500円玉の方がオモテが出た相対度数が大きいことがわかりました。このことから、この表においては「500円玉の方がオモテが出やすい」と言えますね。
確率の求め方は中2で詳しく学習します。
平均値、中央値、最頻値、階級が小6へ移行
誤差や近似値が中3へ移行
~中学数学はここが大きく変わる!~
中2に移行・追加された2項目
中学2年生の数学の改訂では、新しく変わった「データの活用」の章に、高校で扱っていたものから移行や追加された項目があります。
証明の部分も追加されて幅が広くなっています。中1ほどは増えていませんが、気を引き締めていきましょう!
中2に移行・追加された項目は、次の2項目です。
- 反例(図形の証明に追加)
- 四分位範囲と箱ひげ図(高校から移行)
では、それぞれを詳しく見ていきましょう。
~中2数学に移行・追加された項目~
反例
中2からはほとんどの中学生が嫌う「図形の証明」が出てきます。その図形の証明に「反例」が新たに追加されました。
反例を解説させていただくには、証明を少し詳しく知る必要があります。少し長くなりますが、図形の証明について見ていきましょう。
そもそも「証明」ってなに?
証明とは「Aならば」という仮定から始まり、「Bなので」というすでに正しいと認められている根拠(理由)として、「Cである」という結論を出していくこと。
つまり…、
「Aであるなら、Bだから、Cになるんだよ」
という、仮定→根拠→結論まで導き出していくことを証明っていいます。
「AならばCになる」を導き出すために、Bを説明していく感じですね。
では証明の例を一つ紹介します。
アルファベットが出てきても、焦らずにゆっくり確認していきましょう。
∠B=∠Cであることを証明しなさい。
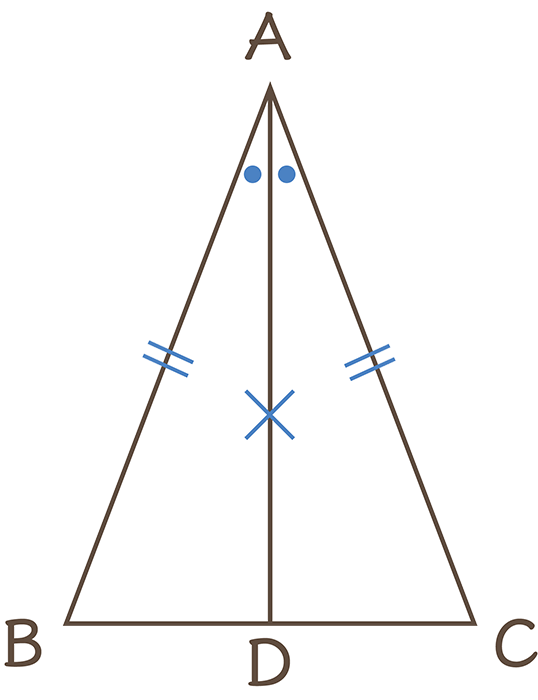
では証明していきます。
∠Aの二等分線を引き、BCとの交点をDとする。
△ABDとACDで、ADは∠Aの二等分線だから、
∠BAD=∠CAD ・・・①
仮定よりAB=AC ・・・②
ADは共通だから、AD=AD・・・③
①、②、③より、△ABDと△ACDにおいて、2組の辺とその間の角がそれぞれ等しいので、△ABD≡△ACD
合同の図形では、対応する角は等しいので、
∠B=∠Cである。
何だか意味の分からない「≡」という記号が出来てきました。「=」に一本線を追加した「≡」です。この記号「≡」は「合同」と読みます。
図形の証明には、よく「合同な図形」というのが出てきます。合同な図形というのは、大きさも形もピッタリ重なる図形のこといいます。つまり、辺の長さや角度が全く同じ図形のことです。
例えば、逆さまな三角形でも、向きを変えたらピッタリ重なる!というのが合同な図形です。その「合同」を表す記号が「≡」なのです。
そして数学では、この重なるという言葉を「対応する」といいます。
先ほどの証明問題で、△ABDと△ACDの2つの三角形で、点Bに対応するのは点Cです。辺の場合は、ABに対応するのはACですね。
次からいよいよ「反例」を紹介します。
反例とは…?
AならばBだとしても、その逆のBならばAになるとは限らない例のことを「反例」といいます。
まずは反例に関係する「逆」についてお話します。
「Aならば、Bである」
これのAとBを逆にしたのが、
「Bならば、Aである」
たとえば、
「二等辺三角形ならば、2つの底角が等しい」
「2つの底角が等しいならば、二等辺三角形である」
「~ならば」が仮定、「~である」が結論です。
二等辺三角形の2つの文章は、どちらもA=Bの関係のことを言っていますが、AとBが逆になっていますよね。この仮定と結論を入れ替えた関係のことを「逆」といいます。
この場合の「逆」については成立しています。2つ目の逆にした文章「2つの底角が等しいならば、二等辺三角形である」は正しいからです。
では、次の「逆」は正しいでしょうか?
△ABCと△DEFで、
△ABC≡△DEFならば、∠A=∠D、∠B=∠E、∠C=∠Fである。
これを逆にすると…、
△ABCと△DEFで、
∠A=∠D、∠B=∠E、∠C=∠Fならば、△ABC≡△DEFである。
この「逆」が正しいかどうか確認をしていきます。
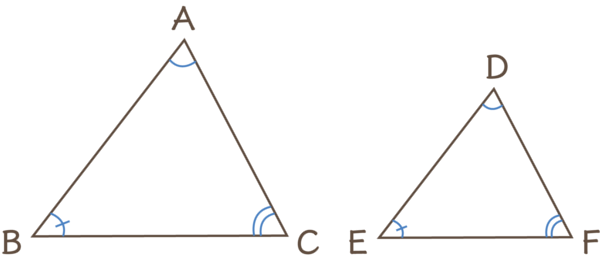
図を見てみると、∠A=∠D、∠B=∠E、∠C=∠Fは当てはまっていますが、△ABCと△DEFが合同であるとは限らないので、正しいとは言えません。

この「逆」については、仮定と結論をただ入れ替えればいいというわけではなく、その逆が本当に正しいかの確認が必要になります。
この結果によって、あることがらが正しくても、その逆が正しいとは限らないということがわかりますよね。
このように、あることがらの仮定に当てはまるもののうち、結論が成り立たない(間違いがある)場合の例を「反例」といいます。
反例はこんな感じで出題されます。
次のことがらの逆をいいなさい。また、それが正しいかどうかを調べて、正しくない場合は反例を示しなさい。
整数A、整数Bで、
AもBも偶数ならば、A+Bは偶数である。
では確認します。
A=2、B=4の偶数なら、A+B=6なので偶数になりますね。
次に逆を確認してみます。
整数A、整数Bで、
A+Bが偶数ならば、AもBも偶数である。
A+B=6の偶数だった場合、AとBには次の組み合わせが考えられます。
A=1、B=5
A=2、B=4
A=3、B=3
A=4、B=2
A=5、B=1
※負の数も入れるともっとありますが…
一番上の「A=1、B=5」の組み合わせが出た時点で奇数ですので、このことがらの「逆」は正しくないことがわかり、「反例」もでました。
一見複雑そうに見えますが、出されたことがらについて、仮定と結論を「逆」にして、それが正しいかを確認し、正しくないならその例を「反例」とするという流れですね。
中2の図形の証明で追加された「反例」ですが、「証明」がちゃんと理解出来れば「反例」はそこまで難しくはないですよ!
~中2数学に移行・追加された項目~
四分位範囲と箱ひげ図
四分位範囲(しぶんいはんい)と、箱ひげ図(はこひげず)が、高校の数Ⅰから中2に移行されました。
中1で学習したヒストグラムと、中2で学習する箱ひげ図。それぞれのグラフの特徴をつかみ、どのような場合にどちらのグラフを使った方が効率的かということも考えられるようにしておくことが必要になってきます。
箱ひげ図とは…?

データの分布をどのあたりの値に集中しているかをひと目で把握することができる図のことです。データが「どれだけ散らばっているか」「どこに偏っているか」が、パッと見でわかるので便利ですよ。

※箱ひげ図は縦に使われることもあります。
中1で学習するヒストグラムとの違いは、複数か1つかの違いです。たとえば、箱ひげ図は、A動物園、B動物園、C動物園の来場者数などの複数のデータを比較することができます。それに対してヒストグラムは、A動物園の年ごとの来場者数の変化が分かるグラフです。
箱ひげ図やヒストグラムは、将来のパソコン作業でプログラミングなどにも活用できるので、初めは難しいと感じるかもしれませんが、ひとつひとつ覚えていきましょう!
四分位範囲とは…?
データを小さい方から並べて4等分したときに、真ん中を含む全体のほぼ50%のデータの散らばりを表したもの。箱ひげ図で箱の部分の範囲、つまり、第3四分位数から第1四分位数を引いた数が「四分位範囲」です。
第1四分位数…?第3四分位数…?
これだけじゃわかりませんよね…。
箱ひげ図で見てみましょう!
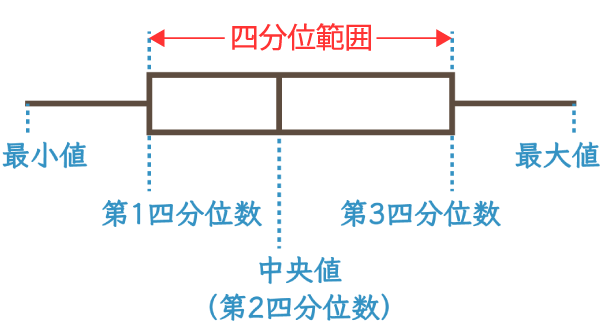
左端を「最小値」といいます。
右端を「最大値」といいます。
全体の真ん中を「中央値」といいます。
中央値は「第2四分位数」ともいいます。
最小値から中央値(前半部分)の真ん中を「第1四分位数」といいます。
中央値から最大値(後半部分)の真ん中を「第3四分位数」といいます。
「第1四分位数」から「第3四分位数」の範囲を「四分位範囲」といいます。
ここでの「真ん中」というのは、箱ひげ図の見た目の真ん中ではなく、データを小さい方から並び替えたときの真ん中にあたる数値のことをいいます。
例えば、「2、3、6、7、15」の5つの数値でしたら、真ん中にある数値は「6」ということがわかりますね。つまり、中央値(第2四分位数)は「6」です。
では「4、6、10、11」の4つの数値の中央値ってわかりますか?真ん中って、6?10?どっち???
数値の個数が偶数個の場合、真ん中の2つの数値の平均値が中央値になります。この場合は、6と10の平均値です。6と10を足して2で割れば求められます。
(6+10)÷2=8
つまり、「4、6、10、11」の中央値は「8」になるというわけです!
箱ひげ図の作成手順
② 中央値(第2四分位数)を求める
③ 第1四分位数を求める
④ 第3四分位数を求める
次のデータは、8人の生徒の数学のテスト結果です。このデータを使って箱ひげ図を作ってみましょう。
8人のテスト結果(点)
( 59、30、62、45、84、51、54、78 )
数字を小さい順に並べるだけです。
( 30、45、51、54、59、62、78、84 )
データが8人分(偶数個)なので、中央値は真ん中にある2つの数値の平均値を求めます。真ん中にある2つの数値は、54と59ですね。
( 30、45、51、54、59、62、78、84 )
54と59の平均値なので、
(54+59)÷2=56.5
中央値(第2四分位数)は「56.5」になります。
第1四分位数は、最小値と中央値の真ん中の数値です。
このテスト結果の最小値は「30」で、中央値は先ほど求めた「56.5」ですが、ここで注意点があります。
第1四分位数(第3四分位数)は、中央値は含めずに求めるということです。
並び替えたデータを見てみます。
( 30、45、51、54、59、62、78、84 )
※中央値56.5
第1四分位数は、中央値56.5を含めない前半部分「30、45、51、54」の真ん中の数値なので、45と51の平均値を計算します。
(45+51)÷2=48
第1四分位数は「48」になります。
第3四分位数は、中央値と最大値の真ん中の数値です。
第3四分位数も第1四分位数と同様に、中央値を含めずに求めます。
並び替えたデータを見てみます。
( 30、45、51、54、59、62、78、84 )
※中央値56.5
第3四分位数は、中央値56.5を含めない後半部分「59、62、78、84」の真ん中の数値なので、62と78の平均値を計算します。
(62+78)÷2=70
第3四分位数は「70」になります。
これで四分位数が全てわかりました!
第1四分位数・・・48
第2四分位数・・・56.5(中央値)
第3四分位数・・・70
実際に箱ひげ図を書いてみましょう!
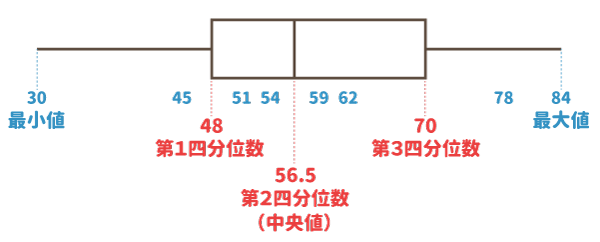
最後に「四分位範囲」を求めてみましょう。
四分位数がわかれば簡単ですよ。
四分位範囲は、第3四分位数から第1四分位数を引いた数なので、
このデータの場合は…
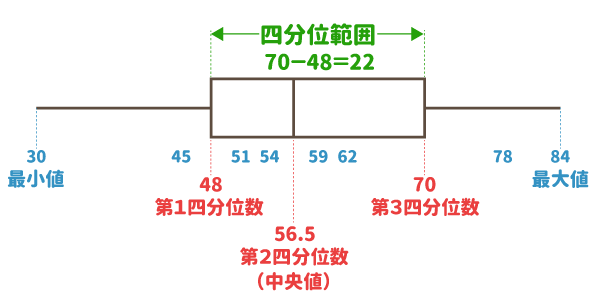
70-48=22
つまり、四分位範囲は22ですね!
箱ひげ図の作成や四分位範囲の求め方を身に付けるには、ひとつひとつの手順を理解した上での練習が大切ですね。
「多数の観察や多数回の試行によって得られる確率」を中1へ移行
~中学数学はここが大きく変わる!~
中3に移行・追加された1項目
中学3年生の数学の改訂では「平方根」の章に、中1で扱っていた「真の値と近似値」が移行されました。
- 真の値と近似値(中1から移行)
~中3数学に移行・追加された項目~
真の値と近似値
中1の資料の活用の章で習っていた「近似値」が、新しい教科書では中3の平方根の章に移行されました。
真の値とか近似値とかって、なんとなく言葉の意味が分かるような気がしますよね。
真の値・・・正確な数値
近似値・・・おおよその数値
その通りです。簡単ですね。
しかし、ここで学習するこの項目は、そんなに単純ではありません。
複雑な計算とかは出てきませんが、言葉の意味がけっこうややこしいので、ひとつひとつ正確に理解を深めていきましょう!
近似値(きんじち)とは…?
近似値とは、簡単に言えばおおよその数値のことですが、もう少し掘り下げて説明しますね!
例えば、消しゴムの長さをミリ単位で計ってみると、25mmでした。
でもこの25mmって正確な数値と言えるのでしょうか?
25.2mmかもしれません。
24.9mmかもしれません。
25.1258mmかもしれません…。
つまり、どんなに精密や定規や計測器で計っても、正確な長さである「真の値」と同じかどうかはわからないのです。
このような不正確な数値(おおよそな数値)を、有効な数値として表したものを『近似値』といいます。
長さや重さなどの測定値だけではなく、円周率(3.14)や、√2なども近似値です。
真の値の範囲
近似値の項目では「真の値の範囲」というものを求める問題がでます。
では、近似値25の真の値を 𝑎 としたときの「真の値の範囲」を求めてみましょう。
ここで必要になるのが四捨五入です。
四捨五入による繰り上げで、25になる最小の数値は「24.5」です。
四捨五入による繰り下げで、25になる最大の数値は「25.4999…」です。
つまり、近似値25の真の値 𝑎 は、24.5以上で25.5未満(※)ということがわかります。
※25.4999…は25.5未満となります。25.4999は25.5を含めないからです。
これで、ある数 𝑎 の小数第1位を四捨五入した近似値が25ならば、𝑎 の範囲はこうなります。
24.5 ≦ 𝑎 < 25.5
不等号の記号に気を付けてください。
24.5以上だから、24.5 ≦ 𝑎
つまり24.5を含めます。
25.5未満だから、𝑎 <25.5
つまり25.5を含めません。
問題はこんな感じででます。
答えはさっき出したやつ。
ちょっと練習してみましょう。
ある数 𝑎 の小数第1位を四捨五入した近似値が37であるとき、𝑎 の範囲を不等号を使って表しなさい。
A. 36.5 ≦ 𝑎 <37.5
ある数 P の小数第2位を四捨五入した近似値が1.7であるとき、P の範囲を不等号を使って表しなさい。
A. 1.65 ≦ P <1.75
誤差の絶対値
真の値の範囲を求める問題では、同時に『誤差の絶対値』を問われることもあります。
ここで言う「誤差」というのは、近似値から真の値を引いた差のことです。
誤差=近似値-真の値
絶対値は中1の正負の数でやりましたね。
符号(+や-)をとった数字だけの部分です。
(例)−5の絶対値は5、+0.7の絶対値は0.7
では、先ほどの、近似値が「25」であるときの「誤差の絶対値」を求めてみましょう。
まず、真の値の範囲を求めます。
ある数 𝑎 の小数第1位を四捨五入した近似値が25ならば、𝑎 の範囲はこうなりましたね。
24.5 ≦ 𝑎 <25.5
誤差と言うのは、近似値-真の値でしたよね。
𝑎 に近似値25を入れて、誤差を出してみます。
24.5 ≦ 𝑎
↑ 𝑎 に25を入れます
24.5 ≦ 25
これで、24.5以上25以下であることがわかるので、その差は0.5以下です。
25-24.5=0.5
もう片方の 𝑎 にも25を入れてみます
𝑎 < 25.5
↑ 𝑎 に25を入れます。
25 < 25.5
これで、25より大きく25.5より小さいので、その差は0.5未満です。
25-25.5=0.5
これで誤差は0.5以下で0.5未満であることがわかりました。
誤差の絶対値は大きいほうを見るので、0.5以下となります。
答え方は、問題の聞かれ方にもよりますが、こう答えます。
Q:誤差の絶対値はいくつか?
A:0.5以下
Q;誤差の絶対値は最大いくつか?
A:0.5
小数第1位を四捨五入した・・・という問題では、誤差の絶対値は必ず「0.5以下」になりますし、少数第2位を四捨五入した・・・という問題なら、誤差の絶対値は「0.05以下」となるわけです。
有効数字とけた数
測定して得られた近似値を表す数で、意味のある数字を『有効数字』といいます。
また、その数字の個数を『有効数字のけた数』といいます。
有効数字とは、確実に信頼が出来る数字のことです。
例えば、消しゴムの長さがを計って「25mm」だとしたら、それは近似値であることは先ほどやりましたよね。
25mmは、もしかしたら25.13mmかもしれないし、24.85mmかもしれないです。計ったときに使った定規だって、少し曲がっていたり、湿度などで縮んでいたりしていたかもしれません。100%正確な定規なんて存在しませんよね。
つまり、消しゴムの長さを計った時の近似値である「25mm」は信頼ができる数字(意味のある数字)ですが、「25.13mm」や「24.85mm」の小数点以下の数字は信頼ができない数字(意味のない数字)であると言えます。
また「25」という数値は「2」と「5」の2つの数字を使っているので、2けたの数字です。つまり、有効数字のけた数は「2けた」ということになります。
では「25」は有効数字でしょうか?
実は、有効数字をはっきりさせた表し方があるので、解説しますね。
有効数字×10n の形
有効数字として表すときには、整数の部分は1ケタだけの小数にして、残りのケタは「×10n」で表すという方法があります。
「25」を有効数字としてはっきりと表すために、以下のようにします。
25は整数部分で2桁なので、整数を1桁の小数にします。
25 → 2.5
2.5にすれば、整数部分は「2」だけの2桁ですね。
次に「×10n」の形にして、正確なけた数を調整します。
2.5 × 10
これで「25」を有効数字として表した形ができました。
「25」を有効数字を表す形にしたら、
2.5 × 10
他にもやってみましょう。
<解説>
有効数字が2桁となっているので、278.13の左から2つの数字だけにします。ここでの注意点は、左から3番目の数字を四捨五入するということです。
有効数字が2桁なので…
278.13の左から2つの数字
=27
278.13の左から3つ目の数字を四捨五入
→8を四捨五入するので切り上げる。
「278.13」を有効数字2桁にして、左から3つめの数字を四捨五入すると「28」になりました。
今度は、整数部分が1桁の小数と10の何乗かの積の形にします。
2.8 × 102
これが、278.13を2桁の有効数字にして、整数部分が1桁の小数と10の何乗かの積の形です。
真の値、近似値、有効数字…、いろいろ難しい言葉が出てきましたね。計算は簡単なものですが、真の値の範囲や、有効数字のけた数など、ややこしいモノも多いので、問題をたくさん解いて慣れていきましょうね。
「素因数分解」を中1へ移行


最後までお読みいただきありがとうございます。ご挨拶が遅れて申し訳ありません。ジャニアスで家庭教師の講師をさせていただいている“さやか”と申します。
このページでは2021年からの新しい学習指導要領で変わった中学校の数学についてお話させていただきました。
これからの中学の数学は「データの活用」が重視されていますね。たくさんの数字やグラフなどのデータから必要なことを読み取る力が必要とされています。
これまで高校で習っていた内容が中学で扱うようになるなど、各段に難しくなりましたよね。私たちが中学生だった時とも、メチャクチャ変わってきています(汗)。
累積度数、箱ひげ図、四分位範囲、近似値…。
数学は難しいと感じる部分がいっぱいあると思います。でも、だからといってわからないところをわからないままには決してしないでもらいたいのです。
今できることは今のうちに解決して、ひとつひとつ確実に解決しながら進んでいく。そのためのサポートを私たち家庭教師のジャニアスは充実させています。
家庭教師のジャニアスでは、お子さんが1人の時の勉強のやり方や、これからどんどん難しくなっていく新しい教科書に対応した勉強法を、無料の体験授業でアドバイスさせていただいています。
「これからの数学が心配で…」
「そもそも勉強が大嫌いで…」
「このままだと高校受験が心配…」
そんなお悩みをお持ちのお母さん!ぜひお気軽に無料の体験授業を試してみてくださいね。
▼ よく見られているページ ▼

家庭教師のジャニアスでは下記の地域にお住いの方に家庭教師を紹介しております。下記に含まれていない地域にお住まいのご家庭でも、家庭教師を紹介できる場合もございますので、お気軽にお問い合わせください。





















































