
“算数”から“数学”へ

小学校のころの算数はいかがでしたか?小数や分数、比や割合、速さ時間道のりなど、取りこぼしはありませんか?
中学からは“算数”から“数学”へと呼び名が変わり、メチャメチャ本格的になります。
小学校で習った算数の基本があやふやなままだと、中学からの数学は立ち行かなくなってしまいます。
中学の数学を学習していく上では、小学校の算数の基本が重要であることをしっかり認識しておきましょう。
中1ではこんなことを学習します。
このページでは、中1数学の絶対に取りこぼしてはいけない「正負の数」「文字の式」「方程式」の学習ポイントをご紹介します!
こんなページも見られています!
>>中学1年生の教科別学習ポイント

2021年4月から中学校の教科書が全面的に改訂され、新しい学習指導要領による授業が開始されました。「数学」は、全ての学年に「データの活用」が追加され、これまで以上にグラフや資料から必要なことを”読み取る力”が重視されています。
もっと詳しく知りたい!
>>2021年からの中学数学はデータだらけ!?

計算の基本!
正負の数について
中学1年生の最初に習う「正負の数」では“数の基本”を勉強します。
ここは“計算の基本”でもあるので、ここでつまずいてしまうと、中学3年間の計算問題が全く分からなくなってしまいますので、絶対に取りこぼしのないようにしてください!!
正負の数では「\(0\) より大きい数」である“ \(+\)(プラス)”と、「 \(0\) より小さい数」である” \(-\)(マイナス)”の概念を勉強します。
まずは“用語”を理解して覚えよう
正負の数では、いきなりたくさんの“用語”が出てきます。
こいつを理解しておかないと、後々に授業で言っていることチンプンカンプンになってしまうので、1つ1つていねいに理解していきましょう

正の数… \(0\) より大きい数( \(0\) は含まない)
負の数… \(0\) より小さい数( \(0\) は含まない)
整数…小数や分数以外の自然な数( \(0\) を含む)
正の整数… \(0\) より大きい整数( \(0\) は含まない)
負の整数… \(0\) より小さい整数( \(0\) は含まない)
自然数… \(0\) より大きい整数(=正の整数)
絶対値…数直線上で \(0\) からの距離( \(+\) や \(-\) の符号を取った数字部分)

たくさんあってややこしいですね…(泣)
ここでは”0(ゼロ)が含まれるか含まれないか”がテストでは狙われやすいですよ!
練習して理解していきましょう!
【問題】以下の数を見て各問に答えなさい
(\(-2\) \(6\) \(-0,2\) \(0\) \(+\)\(\frac{2}{5}\) \(+8\) \(-\)\(\frac{1}{100}\))
問1. 正の数を答えなさい
答え. \(6\) \(+\)\(\frac{2}{5}\) \(+8\)
問2. 負の数を答えなさい
答え. \(-2\) \(-0,2\) \(-\)\(\frac{1}{100}\)
問3. 整数を答えなさい
答え. \(-2\) \(6\) \(0\) \(+8\)
問4. 正の整数を答えなさい
答え. \(6\) \(+8\)
問5. 負の整数を答えなさい
答え. \(-2\)
問6. 自然数を答えなさい
答え. \(6\) \(+8\)
【問題】絶対値について
問1. 次の数の絶対値を答えなさい
(\(-8\) \(+2,5\) \(-\)\(\frac{2}{7}\))
答え. \(8\) \(2,5\) \(\frac{2}{7}\)
問2. 絶対値が \(12\) になる数を全て答えなさい
答え. \(+12\) \(-12\)
他にも正負の数ではムズカシイ呼び名(用語)がたくさん出てきます。

加法(かほう)…たし算のこと
減法(げんぽう)…ひき算のこと
乗法(じょうほう)…かけ算のこと
除法(じょほう)…わり算のこと
四則(しそく)…加法、減法、乗法、除法すべて
※他にも用語はたくさんあります…。

用語はとっても大切です。用語の意味がわからないと、授業中に先生が言っている意味が分からなくなってしまうので、しっかり覚えておきましょうね。
マイナスの概念は不自然だけど重要!
中学から出てくる“マイナスの数”というのは、日常生活では気温やサッカーの得失点差くらいしか思いつきませんよね。
気温なら、-5℃とか、得失点差なら-2点とか…。
しかし、それ以外には日常生活ではマイナスってほとんど使いませんよね。
そもそも「\(0\)より小さい数」ってなんだか変な感じがしませんか…?
だって、ゼロって何にもないからゼロじゃないですか!その何もない“ゼロ”より小さい数って不自然な感じがしますよね。
例えば、これはおかしな問題ですが…
そんなこと言われても…、3つしかないのに5つ食べられませんよね。

計算式で表すと、“ \(3-5\) ”になりますが、小学校では小さい数から大きい数は引けないって習いました。
ところが中1の“正負の数”を勉強すると、\(3-5\) が計算できるようになります。
答えは、\(-2\)。←「マイナス2」って読みます。
※計算上の答えは「 \(-2\) 」と出せますが、クッキーの個数には「\(-2\)個」というのは存在しないので、この問題はお菓子だけにおかしな問題です。(笑ってください…)
ではこれはどうでしょう?
これは気温だけに自然な問題ですね。
(お願い…笑って!)
では計算してみましょう。
\(2-5=-3\) 答え. \(-3\) ℃
このように、\(0\) より小さい“マイナスの数”というのは、普段の日常生活ではあまり出てこない数字ですが、中学数学を学習していく上でとっても大切な概念であることを覚えておきましょう
★計算の基本★
正負の数の「加法と減法」
数直線を使おう!
加法と減法は計算を覚える前に“数直線”を使って理解していきます。
数直線ってこんなのです。
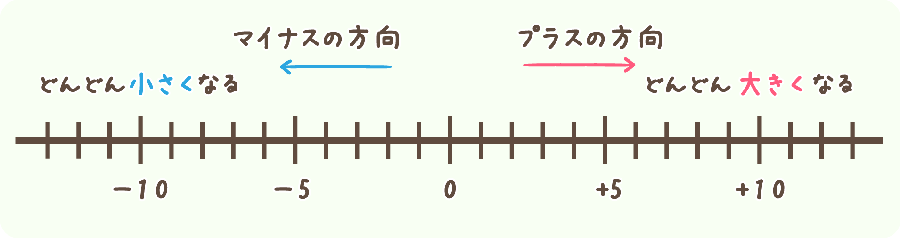
右に向けて大きくなり、左に向けて小さくなります。
右への方向がプラスの方向で、左への方向がマイナスの方向です。
\(0\) より左側が「負の数」、
\(0\) より右側が「正の数」です。
では実際に練習してみましょう。
問題1.
以下の数を数直線上に書きなさい。
\(-7\) \(+2\) \(5,5\) \(-\)\(\frac{1}{2}\)
答え.
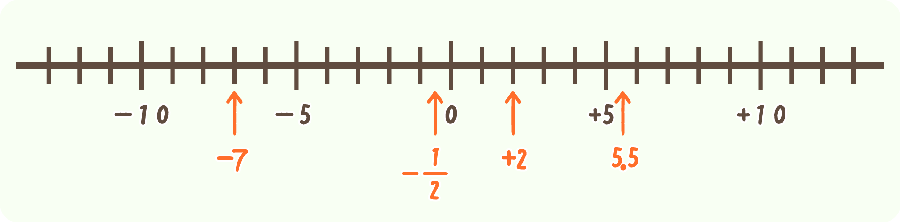
問題2.
数直線を使って以下の計算をしなさい。
\(+2-6\)
\(+2\) \(-\) \(6\)
まず、\(+2\) に注目!!
\(+2\) を数直線上に印をつけてみます。
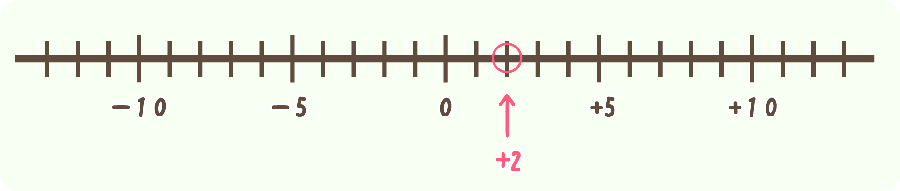
\(+2\) \(-\) \(6\)
次に、\(-6\) に注目!!
印をつけた「\(+2\)」のところから、マイナスの方向(左の方向)に向かって6マス進めます。
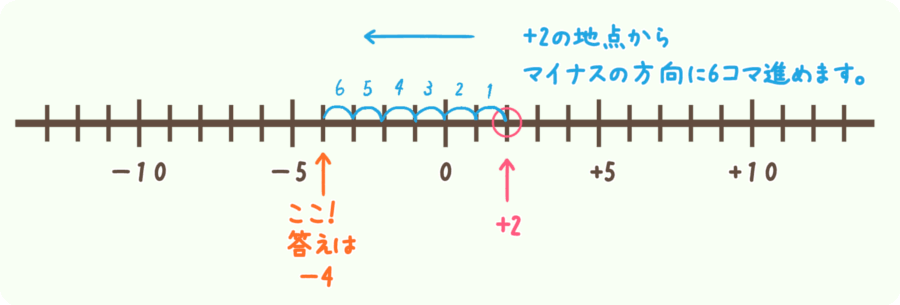
答え. \(-4\)
正負の数の初めのころは、数直線を使っての考え方が大切です。
実際に数直線を見なくても頭の中でイメージできるようになるまで、何度も繰り返し練習しましょう。
数直線を使わないで計算しよう!
次は、数直線を使わないで計算していきます。
同じ符号どうしの加法(たし算)
その符号をつけて、数字の部分(絶対値)を足します。
\((\,+3\,)+(\,+4\,)\) をやってみましょう。
同じプラスの符号のついた加法です。
①同じプラスの符号なので、プラスをつけます。
\(+\) \((\,3+4\,)\)
②次に数字の部分を足します。
\(+\) \((\) \(3+4\) )\(\,=+7\)
※+7はプラスをとって、7でも正解です。
答え. \(7\)
\((\,-7\,)+(\,-2\,)\) はどうでしょう。
同じマイナスの符号がついた加法です。
①同じマイナスの符号なので、マイナスをつけます。
\(-\) \((\,7+2\,)\)
②次に数字の部分を足します。
\(-\) \((\) \(7+2\) \()\,=-9\)
答え. \(-9\)
他にも練習してみましょう!
\((\,+5\,)+(\,+6\,)\)
\(=+\,(\,5+6\,)\)
\(=+11\)( \(11\) でもOK )
答え. \(11\)
\((\,-9\,)+(\,-1\,)\)
\(=-\,(\,9+1\,)\)
\(=-10\)
答え. \(-10\)
\((\,-4\,)+(\,-1\,)\)
\(=-\,(\,4+1\,)\)
\(=-5\)
答え. \(-5\)
違う符号どうしの加法(たし算)
ここから一気に難しくなります。
違う符号の加法は、絶対値の大きいほうの符号をつけて、絶対値の大きいほうの数から小さいほうの数を引きます。
たし算なのに“引く”ところがややこしいんです…。
\((\,-8\,)+(\,+3\,)\) をやってみましょう。
違う符号(マイナスとプラス)がついた加法ですね。
これは計算の手順がちょっと複雑です。
①まず、「 \(-8\) 」と「 \(+3\) 」で、絶対値に注目します。
絶対値は符号を取った数字の部分だけなので、「 \(8\) 」と「 \(3\) 」ですね。
数字の大きいほうは「 \(8\) 」です。
「 \(8\) 」についていた符号は「マイナス」です。
ですので、初めに絶対値の大きいほうについていた符号の「マイナス」をつけます。
\(-\) \((\,8-3\,)\)
②絶対値の大きい数から小さい数を引きます。
\(-\,(\)\(\,8-3\,\)\()\,=-5\)
答え. \(-5\)
他にも練習してみましょう!
\((\,+5\,)+(\,-6\,)\)
\(=-(\,6-5\,)\)
\(=-1\)
答え. \(-1\)
\((\,-8\,)+(\,+2\,)\)
\(=-(\,8-2\,)\)
\(=-6\)
答え. \(-6\)
\((\,-4\,)+(\,+7\,)\)
\(=+(\,7-4\,)\)
\(=+3\)( \(3\) でもOK)
答え. \(3\)
減法(ひき算)について
加法(たし算)については、同じ符号どうしが違う符号どうしかによって計算方法が異なりました。
では減法はどうでしょうか?
ここからは「カッコの外し方」をマスターしていきましょう。
カッコを外すことが出来るようになれば、加法と減法は同じ考え方で計算できるということがわかっちゃいます。
カッコの外し方
カッコを外すときに注目するところは、カッコの直前の部分です。
カッコの直前に何もなければそのままカッコを外すだけ。
\((\,+5\,)\) → \(\,+5\,\)
\((\,-3\,)\) → \(\,-3\,\)
カッコの直前に+(プラス)がある時もそのままカッコを外すだけ。
\(+\,(\,-8\,)\) → \(-8\)
\(+\,(\,+2\,)\) → \(+2\)
カッコの直前に-(マイナス)がある時は、カッコ内の符号を変えてカッコを外す。
(※ここがちょっとやっかいですね…)
\(-\,(\,+5\,)\) → \(-5\)
\(-\,(\,-6\,)\) → \(+6\)
ではこの計算でカッコを外してみましょう。
\((-5)-(+3)\)
まず \((\,-5\,)\) のカッコを外します。
\((\)\(\,-5\,\)\()\)\(-\,(+3\,)\)
\((\,-5\,)\) の直前には何もないのでそのままカッコを外すだけ。
\(-5-(\,+3\,)\)
次に \((\,+3\,)\) のカッコを外します。
\(-5\,-\,\)\((\)\(\,+3\,\)\()\)
\((\,+3\,)\) の直前にはマイナスがありますよね。
カッコの直前にマイナスがある時は、カッコ内の符号を変えてカッコを外します。
\(-5-3\)
だいぶスッキリしましたね。
もちろんここままでも計算できますが、ちょっとていねいにカッコをつけてみます。
「せっかく外したカッコをつけるの?」って思うかもしれませんが…
カッコをつけるには、それぞれにカッコをつけて、+でつなげます。
\(-5-3\)
\(=\,\)\((\)\(\,-5\,\)\()\,+\,(\)\(\,-3\,\)\()\)
こうすると、初めの式の
\((\,-5\,)-(\,+3\,)\) が、
\((\,-5\,)+(\,-3\,)\) になりました。
減法が加法になりましたね。
あとは、計算するだけ。
\((\,-5\,)+(\,-3\,)\)
\(=-(\,5+3\,)\)
\(=-8\)
答え. \(-8\)
カッコを外してそのまま計算する

先ほどのカッコのついた減法の計算では、一度カッコを外してスッキリさせてから、さらにカッコをつけて“プラス”で結んで計算しました。
ここでは、カッコを外した状態で計算していきます。
\(-8-(\,-2\,)\)
まずはカッコを外します。
カッコの前に“マイナス”があるので、カッコ内の符号を変えてカッコを外します。
\(-8-(\,-2\,)\)
\(=-8+2\)
ここで、加法の計算を思い出してください。
<同じ符号どうし>
→その符号をつけて絶対値を足す。
<違う符号どうし>
→絶対値の大きいほうの符号をつけて、大きい絶対値から小さい絶対値を引く。
\(-8+2\) の式は、\(-8\) と \(+2\) なので、違う符号どうしですよね。
\(-8\) と \(+2\) の絶対値は \(8\) と \(2\) です。\(8\) のほうが大きいので、\(8\) についている符号のマイナスをつけてから、\(8-2\) をします。
\(-8-(\,-2\,)\)
\(=-8+2\)
\(=-(\,8-2\,)\)
\(=-6\)
答え. \(-6\)
ではこの計算はどうでしょう。
\(-12-7\)
\(-12\) と \(-7\) なので、同じ符号どうしですね。
同じ符号どうしの場合は、その符号をつけてから絶対値を足します。
\(-12-7\)
\(=-(\,12+7\,)\)
\(=-19\)
答え. \(-19\)
少し複雑な計算をやってみましょう!
\(-5-(\,-2\,)+(\,-8\,)+3\)
①カッコを外しましょう。
※カッコの直前がプラスならカッコ内の符号を変えずに外します。
※カッコの直前がマイナスならカッコ内の符号を変えて外します。
\(-5-(\,-2\,)+(\,-8\,)+3\)
\(=-5+2-8+3\)
カッコが外れました!
②計算がしやすいように、同じ符号どうしで順番を変えちゃいましょう。
※カッコが外れた式は“加法の式”ということになります。
加法は計算の順番を変えても大丈夫です。たとえば、「5+2」と「2+5」って同じ7になりますよね。
このことを“加法の交換法則”っていいます。
\(-5-(\,-2\,)+(\,-8\,)+3\)
\(=-5+2-8+3\)
\(=\,\)\(-5-8\) \(+2+3\)
順番を変えました!
③マイナスどうしとプラスどうしをそれぞれ計算します。
\(-5-(\,-2\,)+(\,-8\,)+3\)
\(=-5+2-8+3\)
\(=-5-8+2+3\)
\(=\) \(-\,(\,5+8\,)+(\,2+3\,)\)
\(=-13+5\)
④最後に残った式は「\(-13+5\)」ですね。
これは違う符号どうしなので、絶対値が大きい方についている符号をつけて、絶対値の大きい数から小さい数を引きます。
\(-5-(\,-2\,)+(\,-8\,)+3\)
\(=-5+2-8+3\)
\(=-5-8+2+3\)
\(=-\,(\,5+8\,)+(\,2+3\,)\)
\(=-13+5\)
\(=\) \(-(\,13-5\,)\)
\(=-8\)
答え. \(-8\)
ここまで正負の数の“加法と減法”をご紹介しました。
次は“乗法と除法”をご説明いたします。
★計算の基本★
正負の数の「乗法と除法」
乗法(かけ算)、除法(わり算)の計算は、加法・減法よりもカンタンです!
一気にやっちゃいましょう!!
手順はたったの2つ。
②数字部分を計算する
たったのこれだけ!カンタンです。
符号の決め方はこうしよう。
ここでは乗法(かけ算)で説明しますね。
同じ符号どうし
\((\,+\,)×(\,+\,)\) や \((\,-\,)×(\,-\,)\) なら!
符号は「\(+\)」
違う符号どうし
\((\,+\,)×(\,-\,)\) や \((\,-\,)×(\,+\,)\) なら!
符号は「-」
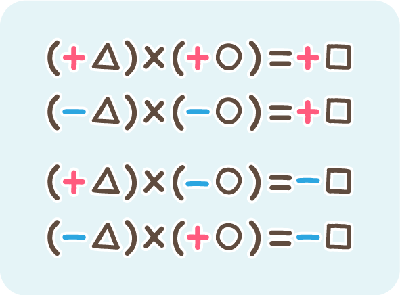
同じ符号どうし
\((\,+\,)×(\,+\,)\) や \((\,-\,)×(\,-\,)\) なら!符号は「\(+\)」
違う符号どうし
\((\,+\,)×(\,-\,)\) や \((\,-\,)×(\,+\,)\) なら!符号は「-」
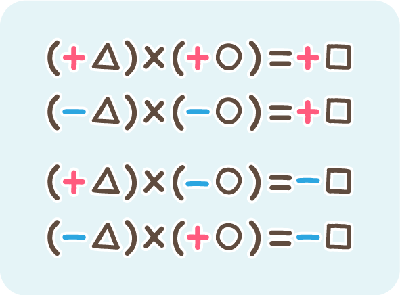
では実際にやってみましょう!
\((\,-6\,)×(\,-3\,)\)
同じマイナスどうしなので、符号はプラスになります。
あとは「\(6×3\)」を計算するだけ。
\((\,-6\,)×(\,-3\,)\)
\(=+18\)( \(18\)でもOK )
答え. \(18\)
\((\,+5\,)×(\,-2\,)\)
プラスとマイナスで違う符号どうしですね。その場合の符号はマイナスになります。
\((\,+5\,)×(\,-2\,)\)
\(=-10\)
答え. \(-10\)
除法(わり算)も同じです。
\((\,-8\,)÷(\,-2\,)\)
同じマイナスどうしなので、符号はプラスになります。
あとは「\(8÷2\)」を計算するだけ。
\((\,-8\,)÷(\,-2\,)\)
\(=+4\)( \(4\)でもOK )
答え. \(4\)
\(12÷(\,-3\,)\)
これは違う符号どうしなので、符号はマイナスになります。
※\(12\)には符号が付いていませんが、+が省略されています。
\(12÷(\,-3\,)\)
\(=-4\)
答え. \(-4\)
ではこんな計算はどうでしょう?
\(-2×4×(\,-3\,)×(\,-1\,)\)
長い式ですね。
こういう場合は、すべてかけ算(わり算)であることを確認した上で、マイナスがいくつあるか数えましょう。
※プラスは省略できますがマイナスは省略できないので、マイナスの数を数えた方がいいです。
乗法・除法はマイナスの数によってプラスになるかマイナスになるかを決められます。
マイナスの数が奇数ならマイナス
マイナスの数が偶数ならプラス
マイナスの数が0個ならプラス
\(-\)\(2×4×(\)\(-\)\(3)×(\)\(-\)\(1)\)
マイナスが3つありますよね。
3つということは奇数ですので、符号はマイナスになります。
あとは、数字を計算してマイナスをつけます。
\(2×4×3×1=24\)
答え. \(-24\)
★計算の基本★
四則が混じった計算
ここからは四則計算をやっていきます。
四則(しそく)とは、加法・減法・乗法・除法のことでした。
数学の用語って難しいですが、しっかり覚えていきましょうね。
次の式は、加法と除法が混じっています…。
\(-5+8÷(-2)\)
計算する順序に注目!
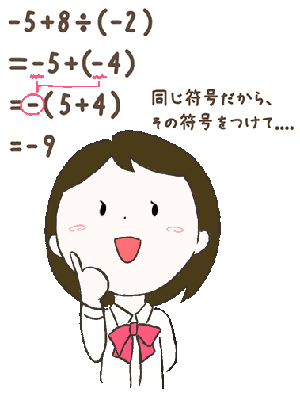
“たし算・ひき算”と“かけ算・わり算”が混じった計算の場合は、必ず、“かけ算・わり算”から先に計算します。
小学校の算数でもやりましたよね。
\(-5+8÷(-2)\) の計算は、まず、
\(+8÷(\,-2\,)\) を先に計算します。
\(-5\)\(+8÷(\,-2\,)\)
\(=-5\)\(-4\)
\(=-9\)
答え. \(-9\)
この計算はどうでしょう。
\(3+5×(-2)-8÷2\)
\(+5×(-2)\) と \(-8÷2\) をそれぞれ先に計算します。
\(3\) \(+5×(-2)\) \(-8÷2\)
\(=3\) \(-10\) \(-4\)
\(=-11\)
答え. \(-11\)
少し練習してみましょう。
(1)\(5-1×3-(\,-5\,)×(\,-2\,)\)
(2)\(-6-2×6+8÷(\,-4\,)\)
(3)\(9+2×(\,-6\,)-2-4÷2\)
解説(1)
\(5-1×3\)\(\,-\,(\,-5\,)\)\(\,×\,(\,-2\,)\,\)
<不要なカッコを外します>
\(=5-1×3\)\(\,+\,5\,\)\(\,×\,(\,-2\,)\)
\(=5\)\(\,-\,1×3\)\(\,+\,5×(\,-2\,)\,\)
<かけ算を先に計算します>
\(=5\)\(\,-\,3\,\)\(-10\)
\(=-8\)
答え. \(-8\)
解説(2)
\(-6\)\(\,-2×6\)\(\,+8÷(\,-4\,)\,\)
<かけ算とわり算を先に計算します>
\(=-6\)\(\,-12\,\)\(-\,2\)
\(=-20\)
答え. \(-20\)
解説(3)
\(9\)\(\,+2×(\,-6\,)\)\(\,-2\)\(\,-4÷2\,\)
<かけ算とわり算を先に計算します>
\(=9\)\(\,-12\)\(\,-2\)\(\,-2\)
\(=-7\)
答え. \(-7\)
正負の数は「習うより慣れろ」です。
たくさん計算練習をして、絶対に取りこぼしのないようにしていきましょう!
式を作る基本!
文字式について
小学校の頃にも少し出てきた「\(\,x\,\)」とか「\(\,y\,\)」を使った式が、中学から本格的になり、この後で出てくる”方程式”を理解する上で、メチャメチャ大事な基本となります。
でも文字式はルールさえ覚えてしまえばカンタン!
まずは絶対に抑えておきたい、文字式のルールをご説明いたします。
★式を作る基本★
文字式のルール
① かけ算は「×」を省略する。
② わり算は「÷」を省略して分数で表す。
③ 同じ文字のかけ算は「指数」を使って表す。
④ 1や-1と文字のかけ算は「1を省略」する。
⑤ カッコの式と文字や数字のかけ算はカッコの式の前におく。
① かけ算は「\(×\)」を省略する
文字を含むかけ算は、\(×\)を省略して書きます。
\(a×b\) は「\(×\)」を省略して \(ab\) と書きます。
\(x×y\) は \(xy\)
\(2×a\) は \(2a\)
\(×\)を省略したときの順序にもルールがあります。
・数字は前に書く
・アルファベット順に書く
\(a×3\) は \(a3\) とは書かずに \(3a\) と書きます。
\(b×a\) は、\(ba\) とは書かずに \(ab\) と書きます。
\(y×2×x\) は \(2xy\) となります。
② わり算は「\(÷\)」を省略して分数に
文字を含むわり算は、\(÷\)を省略して分数で表します。
\(a÷b\) は \(\frac{a}{b}\) と書きます。
\(x÷2\) は \(\frac{x}{2}\) と書きます。
わり算は必ず、わる数が分母、わられる数が分子になります。
③ 同じ文字のかけ算は「指数」を使う
同じ文字を何度かかける時は、文字の右上にかける回数(指数)を使って表します。
\(x×x\) は、\(x^2\) ( \(x\) の2乗)
\(a×a×a\) は、\(a^3\) ( \(a\) の3乗)
こんなのも覚えていきましょう。
\((x+2)×(x+2)\)は、\((x+2)^2\)
\((a-3)×(a-3)×(a-3)\)は、\((a-3)^3\)
④ 1や-1と文字のかけ算は1を省略する

\(1\) や \(-1\) と文字のかけ算は、\(1\) を省略して書きます。
\(1×a\)は「\(1a\)」とはせず「\(a\)」となります。
\(-1×b\)は「\(-1b\)」とはせず「\(-b\)」となります。
しかし、\(0,1\) や \(0,01\) の \(1\) は省略しません。
\(0,1×a\)は、\(0,1a\) となります。
(\(0,a\) とはなりません)
\(0,01×b\)は、\(0,01b\) となります。
(\(0,0b\) とはなりません)
⑤ カッコが付いている式とのかけ算は「\(×\)」を省略してカッコの前に書く
\(-3×(x+y)\)
これはカッコの式に \(-3\) がかけられていますね。
この場合は \(×\) を省略してこうなります。
\(-3(x+y)\)
これはどうでしょう。
\((a-b)×5\)
この場合も \(×\) を省略しますが「\(5\)」をカッコの前に書きます。
\(5(a-b)\)
ではここまでお話しした5つのルールを同時に利用した問題を解いてみましょう。
問1.
\((5+y)×a×a×3×b×a\)
長い計算問題ですが手順通りにやれば大丈夫!
かけ算の順番は、数字が先頭、あとはアルファベット順、さらに同じものをかけているときは指数を使います。さらに式がカッコでくくられているときは、最後になります。
① 順番を変えます。
\(3×a×a×a×b×(5+y)\)
②\(×\)を省略します。
\(3a^3b(5+y)\)
答え. \(3a^3b(5+y)\)
問2.
\((x-2)×(x-2)×y×(-3)\)
これもやばそうですね。カッコの式が2個あったり…。
順番通りにやってみましょう。
① 順番を変えます。
\(-3×y×(x-2)×(x-2)\)
② \(×\)を省略します。
\((x-2)×(x-2)\)は2乗で表します。
\(-3y(x-2)^2\)
答え. \(-3y(x-2)^2\)
問3.
\(a×b÷2\)
今度はかけ算とわり算が混じっています。
① まず \(×\) を省略します。
\(ab÷2\)
② 次に \(÷\) を分数にします。
\(\frac{ab}{2}\)
答え. \(\frac{ab}{2}\)
★式を作る基本★
文字式の文章問題
文字式のルールはちゃんと理解できましたか?
ここからは“文字式の文章問題”をお話ししていきます。
文章問題って聞いて何となくイヤな予感がしてしまう中学生も多いかと思います。
数学がキライな中学生が、最も苦手にしてしまうのが文章問題なんです。
文章問題は、文章を読み解いて“自分で式をつくる”ところが厄介ですよね。
ここでつまずいてしまうと、この後に出てくる方程式で必ず苦労するので、文字式の文章問題のところで確実に理解しておきましょう。
<問1>
「1個60円の消しゴムを \(x\) 個買った時の代金を文字式で表せ」
<問2>
「1本 \(y\) 円のボールペンを5個買った時の代金を文字式で表せ」

これは小学校の頃にもやったと思いますが、普段の生活では、\(x\) 個とか \(y\) 円とかって絶対に使いませんよね。
普段は、3個とか500円とか実際の数字を使って表しています。
文字を使った式を作るには、文字の所に実際の数字(かんたんな数字)をあてはめてみるとわかりやすくなります。
<問1>
「1個60円の消しゴムを \(x\) 個買った時の代金を文字式で表せ」
この \(x\) 個のところを3個にしてみたらどうでしょう?
「1個60円の消しゴムを3個買った時の代金を文字式で表せ」
これなら簡単じゃないですか?
\(60×3=180\)
では、3個を元々の \(x\) 個に戻しましょう。
すると・・・
\(60×x=60x\)
答え. \(60x\) 円
<問2>
「1本 \(y\) 円のボールペンを5個買った時の代金を文字式で表せ」
これも、\(y\) 円の所を100円にしてみます。
\(100×5=500\)
では100円のところを元々の \(y\) 円に戻して式を作ります。
\(x×5=5x\)
答え. \(5y\) 円
このように、初めのうちは文字のところに簡単な数字を入れて考えてみるとわかりやすくなりますよ。
ではここでやった<問1>と<問2>が混ざった問題をやってみましょう。
だんだん難しくなります…。
<問3>
「1個60円の消しゴムを \(x\) 個と、1本 \(y\) 円のボールペンを5個買った時の合計金額を文字式で表せ」
文章が長くなりましたね。長い文章問題は、ひとつひとつ文章を区切って考えるのが大切です。
この問題では「1個60円の消しゴムを \(x\) 個」というのと「1本 \(y\) 円のボールペンを5個」で分けられます。
それぞれ式を作ります。
「1個60円の消しゴムを \(x\) 個」
これは、\(60×x\) なので、① \(60x\) です。
「1本 \(y\) 円のボールペンを5個」
これは \(y×5\) なので、② \(5y\) です。
①と②の合計金額なので、\(60x+5y\)ですね。
答え. \(60x+5y\) 円
文字式の速さの問題
さらに一気に難しくなります…。
速さの問題って小学校でもみんなつまずくところですが、中学でも思いっきり出てきます!
速さを求める公式は覚えていますか?
「み・は・じ」とか「は・じ・き」でやりましたよね!

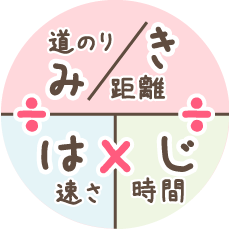
覚えていない子は、まずこれだけは覚えてください。
道のり=速さ×時間
こいつを覚えておけば、速さや時間を求める問題でも、かけ算の逆のわり算で求められます。
速さ=道のり÷時間
時間=道のり÷速さ
では行ってみましょう!
<問題>
自宅からA地点まで、行きの道のりは \(x\) メートル、帰りの道のりは \(y\) メートルです。行きは分速70m、帰りは分速80mで往復しました。往復にかかった時間を文字式で表しなさい。
「往復にかかった時間」ということは「行きにかかった時間」+「帰りにかかった時間」ということになります。
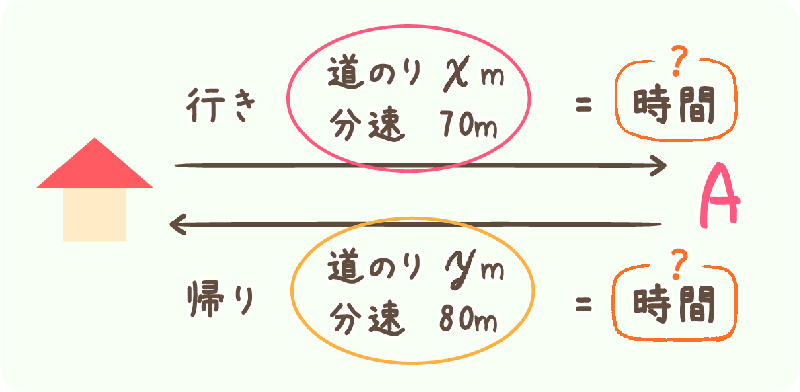
時間を求める問題ですので、
「時間=道のり÷速さ」を使います。
まず、「行きにかかった時間」を求めます。
道のりが \(x\) メートル、速さが分速70mで、時間は、「道のり÷速さ」なので、
\(x÷70=\)\(\frac{x}{70}\) …①
次に、「帰りにかかった時間」を求めます。
道のりが \(y\) メートル、速さが分速80mで、時間は、「道のり÷速さ」なので、
\(y÷80=\)\(\frac{y}{80}\) …②
求めるものは往復の合計時間なので、①+②の式が答えになります。
答え. \( \frac{x}{70} \)+\( \frac{y}{80} \)(分)
文章問題は他にもたくさんのパターンがありますし、いくらでも難しく作れちゃう厄介な問題です。
この辺りから「数学なんて大きらい!」ってなってしまうお子さんも多いので、ちゃんと学校の授業を聞いて分からない所はその都度質問して解決していきましょう。
本格的な数学の始まり
方程式について
方程式から超本格的な“数学”になっていきます。
さらに!中1の「方程式」が中2になると「連立方程式」になり、中3になると「二次方程式」と、どんどん内容が難しくなっていきます。
中1の方程式が理解できるかどうかが、数学を得意教科に出来るかの重要ポイントになるんです!
方程式っていうのはこんなのです。
\(x+3=5\)
\(x\) に何の数字が入るかを求めていきます。
小学校ではこんな感じで出ませんでしたか?
□\(\,+\,3=5\)
□に入る数字は「2」ですね。
つまり・・・
\(x+3=5\) の答えは、
\(x=2\) になります。
「なーんだ、カンタンじゃん!!」
って思うかもしれませんが、決して方程式を侮ってはいけません!!
方程式を解くための“手順”をちゃんと理解しておかないと、複雑な式になったときに訳わかんなくなっちゃいます。
ではゆっくり解説していきますね。
★方程式★
等式の性質
等式というのは =(イコール)で結ばれた式 のことを言います。
さっきの、\(x+3=5\) も、イコールで結ばれている式なので“等式”ですね。
他にも、\(5+1=6\)、\(2×5=10\)、\(x=5\)、\(a+b=c\)、\(a+1=b-5\) なんかも、ぜんぶ“等式”です。
また、イコールの左側を“左辺”といい、右側を“右辺”といいます。
さらに、左辺と右辺の両方を“両辺”っていいます。
この等式にはとっても重要な4つの性質があるんです。
等式の性質
例えば、ここにA君とB君の双子の兄弟がいて、二人は毎月1,000ずつお小遣いをもらっています。
同じ金額のお小遣いなので、等式が成り立ちますね。
1,000円(A君のお小遣い)=1,000円(B君のお小遣い)
 ある月にお母さんが、「今月はご褒美に2人ともお小遣いを500円アップするわ!」って言ってくれました。これは嬉しいですね。
ある月にお母さんが、「今月はご褒美に2人ともお小遣いを500円アップするわ!」って言ってくれました。これは嬉しいですね。

1,000+500=1,000+500
さらにある月に「今月は二人とも成績が上がったからお小遣いを2倍にするわ!」って言いました。最高ですね!!
2人ともお小遣いが2倍(×2)なので、式はこうなります。
1,000×2=1,000×2
今度は、「今月はお手伝いをサボったからお小遣いを200円減らすわ!」と言われました。キツイですね…(泣)
2人ともお小遣いがマイナス200円なので、式はこうなります。
1,000-200=1,000-200
 さらに…「2人とも成績が下がったから今月のお小遣いは半分よ!」
さらに…「2人とも成績が下がったから今月のお小遣いは半分よ!」
こ、これはきつ過ぎる…(号泣)

1,000÷2=1,000÷2
つまり・・・
イコールで結ばれた等式は、両辺に同じ数を足しても、引いても、かけても、割っても、等式が成り立つ(左辺と右辺が同じ大きさ)というのが“等式の性質”なのです。
教科書にはこう書いてあります。
A=Bならば、A+C=B+C
A=Bならば、A-C=B-C
A=Bならば、A×C=B×C
A=Bならば、A÷C=B÷C
AとかBとかややこしいので、等式の性質は「双子のお小遣い」で覚えておきましょう。
等式の性質を使って方程式を解く
\(x+3=5\)
ではこの方程式を「等式の性質」を使って解いてみましょう。
まず、方程式というのは、求める文字の部分(この式だと \(x\) ですね)に何の数字が入るかを求めていく式です。
つまり、最終的には、
「\(x=\)」の形にしていきます。
「\(x=\)」の形にするには「\(+3\)」が邪魔なのでこいつを消します。
「\(+3\)」を消すには、「\(-3\)」すればゼロになるので両辺に「\(-3\)」を追加します。
\(x+3\) \(-3\) \(=5\) \(-3\)
これを計算すると、
\(x=2\) となりますね。
答え. \(x=2\)
ではいくつかやってみましょう。
\(x-5=7\)
こいつも「\(x=\)」の形にします。左辺の「\(-5\)」を消したいので、両辺に「\(+5\)」をします。
\(x-5\) \(+5\) \(=7\) \(+5\)
これを計算するとこうなります。
\(x=12\)
答え. \(x=12\)
これはどうでしょう?
\(3x=9\)
\(3x\) の \(3\) の部分が消えれば「\(x=\)」の形になりますが、\(3x\) というのは「\(x×3\)」のことです。つまり「\(×3\)」を消すには反対の「\(÷3\)」をすればいいんです。
\(3÷3\) は \(1\) になりますよね。\(1×x\) は「\(x\)」になります。( \(1\) は省略するので)
では両辺に「\(÷3\)」をします。
\(3x\) \(÷3\) \(=9\) \(÷3\)
これを計算すると、
\(x=3\)
答え. \(x=3\)
最後はこんなやつです。
\(\frac{x}{4}\)\(=3\)
みんなが嫌いな分数です。
\(\frac{x}{4}\)ってことは、\(x÷4\) です。「\(÷4\)」を消すには反対の「\(×4\)」をします。
では両辺に「\(×4\)」をしてみましょう。
\(\frac{x}{4}\)\(×4\)\(=3\)\(×4\)
これを計算すると、
\(x=12\)
答え. \(x=12\)
このように方程式は、両辺に同じ数字を足したり引いたり掛けたり割ったりする“等式の法則”を使って解くことができます。
★方程式★
移項(いこう)
「等式の性質」を使って解くときは、両辺に同じ数字を足したり引いたりしましたよね。
ただこの解き方はミスが起こりやすく、例えば左辺に \(-5\) をしたけど右辺を忘れてそのままにしてしまう…、そんなミスです。
<間違い>
\(x+5=8\)
\(x+5\) \(-5\) \(=8\)
\(x=8\)
<正解>
\(x+5=8\)
\(x+5\) \(-5\) \(=8\) \(-5\)
\(x=3\)
左の<間違い>は、右辺に「\(-5\)」を忘れていますね…
そこで、等式の性質を使うやり方よりも、もっと簡単にミスしにくい解き方が“移項”ってやつです。すごく便利な解き方なので慣れていくと楽しくなりますよ。
しかし!移項を覚える前には必ず“等式の性質”を理解しておく必要があります。
“等式の性質”を簡単に省略したのが“移項”だからです。
移項(いこう)とは…?
教科書にはこう書いてあります。
等式では一方の辺の項を符号を変えて他方の辺に移すことができます。このことを移行するといいます。
この方程式でやってみましょう。
\(x+3=5\)
等式の性質で解くと…
方程式は、\(x=\) の形にするので、「\(+3\)」を消すために、両辺に「\(-3\)」をつけます。
\(x+3=5\)
\(x+3\) \(-3\) \(=5\) \(-3\)
\(x=2\)
移項で解くと…

\(x+3=5\)
\(x=5\) \(-3\)
\(x=2\)
計算がシンプルになりました。
よく見ると、左辺の \(+3\) を \(-3\) に変えて右辺に移動していますね。
これを「符号を変えて他方の辺に移す」ということで、移項って言います。
左辺から右辺だけではなく、逆の右辺から左辺へも移項ができます。
方程式は「\(x=\)」の形にしていくので、\(x\) のついた項は左辺に、数字だけの項を右辺に移項します。
\(2x=\) \(4x\) \(+12\)
\(2x\) \(-4x\) \(=12\)
\(-2\)\(x=12\)
\(x=12\) \(÷\,(-2)\)
\(x=-6\)
\(3x\) \(-1\) \(=\) \(5x\) \(+7\)
\(3x\) \(-5x\) \(=7\)\(+1\)
\(-2\)\(x=8\)
\(x=8\) \(÷\,(-2)\)
\(x=-4\)
移項した時の符号の変化は4パターンです。
=(イコール)の橋をこえた時には、以下のように符号が変化することを覚えておきましょう。
① \(+\)(プラス)は\(-\)(マイナス)になる
② \(-\)(マイナス)は\(+\)(プラス)になる
③ \(×\)(かける)は\(÷\)(割る)になる
④ \(÷\)(割る)は\(×\)(かける)になる
いろいろな方程式を解こう!
<カッコのついた方程式>
\(2(3x+2)=-14\)
カッコがある式はまずカッコを外します。
\(2(3x+2)\) のカッコを外しますが、この場合はカッコ内の全てに \(2\) をかけます。
これを“分配法則”っていいます。
\(2(3x+2)=-14\)
\(6x+4=-14\)
\(6x=-14-4\)
\(6x=-18\)
\(6x=-18÷6\)
\(x=-3\)
<小数が入った方程式>
\(-0,3x+0,4=1\)
小数のままでも計算できますが、ややこしくなりますしミスしやすいです。
小数が入った方程式の場合は、両辺に \(10\) や \(100\) をかけて整数にします。
この式の場合は、\(-0,3\) と \(0,4\) があるので、両辺に \(10\) をかけます。
\(-0,3x+0,4=1\)
\(10×\)\((-0.3x+0,4)=\)\(10×\)\(1\)
\(-3x+4=10\)
\(-3x=10-4\)
\(-3x=6\)
\(x=-2\)
<分数が入った方程式>
\(\frac{(x+1)}{2}\)\(\,=\,\)\(\frac{1}{5}\)\(x+2\)
分数を含む方程式は、分母の最小公倍数を両辺にかけて分数を含まない形にします。
この式の分母は \(2\) と \(5\) ですね。\(2\) と \(5\) の最小公倍数は \(10\) です。
では両辺に \(10\) をかけてみましょう。
\(\frac{(x+1)}{2}\)\(\,=\,\)\(\frac{1}{5}\)\(x+2\)
\(10×\)\(\frac{(x+1)}{2}\)\(\,=\,\)\(10×\)\((\)\(\frac{1}{5}\)\(x+2)\)
\(\frac{(10x+10)}{2}\)\(\,=\,\)\(\frac{10}{5}\)\(x+20\)
\(5x+5=2x+20\)
\(5x-2x=20-5\)
\(3x=15\)
\(x=5\)
★方程式★
文章問題
方程式の計算が出来るようになったら、次は文章問題にチャレンジです。
ここでつまずいて「数学なんて大嫌い!」ってなっちゃう子も多いですが、ちゃんと手順を意識して式を作っていけば大丈夫ですよ!
では問題です。
文章問題を解くには手順が大切です。次の手順をひとつひとつ確認しながら解いていきましょう。
<手順①>
数量の関係を見つけて等式を作ります。
この問題の“代金の関係”はこうですね。
「ノート5冊」と「消しゴム1個」の代金
=「ノート1冊」と「ボールペン1本」の代金 ×3
<手順②>
まだわかっていない数量(未知数といいます)を文字であらわして方程式をつくります。
文字は何にしてもいいですが、一般的には \(x\) とします。
ここでは求めるものである「ノート1冊の代金」を \(x\) (円)として方程式を作ります。
\(5x+90=3(x+130)\)
<手順③>
方程式を解きます。
\(5x+90=3(x+130)\)
\(5x+90=3x+390\)
\(5x-3x=390-90\)
\(2x=300\)
\(x=150\)
<手順④>
方程式の解が問題にあっているか調べます。
ノート1冊が150円として、問題文にあてはめてみましょう。
(150円のノートが5冊と90円の消しゴムの代金)は・・・
\(150×5+90=840\) 円
(150円のノート1冊と130円のボールペンの代金)の3倍は・・・
\((150+130)×3=840\) 円
数量の関係で、同じ代金(840円)になったので、問題に合っている。
<手順⑤>
単位をつけて答えを書きます。
\(x=150\) というのは、方程式の解であって、この文章問題の答えではありません。
問題では「ノート1冊の代金を求めなさい」と言われているので、かならず単位(この場合は“円”)をつけて答えを書きましょう。
答え. 150円
方程式の文章問題は、他にもたくさんのパターンがあります。
速さの問題、食塩水の問題、過不足の問題、年齢の問題、他にも方程式っていくらでも文章問題がつくれちゃいます…(汗)
ムチャクチャ難しい問題が平気で出てきますので、色んなパターンの問題をたくさん解いて、ひとつひとつ自分のものにしていきましょう。
(ここからどんどん差が付きますよ!)

このページでは、中学1年生の数学で押さえておきたい重要ポイントである“正負の数”、“文字式”、“方程式”について説明させていただきました。
もちろん方程式の後に習う、“関数”や“図形”も超大事です!
数学はいくらでも応用問題が作れてしまう恐ろしい教科です。
そこに対抗していくには、“基礎の土台”が超重要!
基礎を完璧に理解していけば、あとは練習を重ねることによってどんどん数学が面白くなっていきますよ!
「数学がわからなかくなっている…」
「数学なんて大っキライ!」
そんなお子さんは今すぐ対策をしていかないと、学年が上がるにつれてどんどん勉強が大変になってしまいます。

私たち家庭教師のジャニアスでは、“数学の楽しさ”を教えてたくさんのお子さんに点数アップ、成績アップの結果を出してきました。
今なら!無料の体験授業で勉強のやり方から丁寧に教えていますので、この機会に一度試してみませんか?
もちろん、体験授業を受けていただいたからといって、ご入会への無理な勧誘は一切ありませんのでご安心ください。
体験授業でお会いできることをスタッフ一同、楽しみにしています。

今ご覧になっているページは
数学(中1)です。
▼ よく見られているページ ▼

家庭教師のジャニアスでは下記の地域にお住いの方に家庭教師を紹介しております。下記に含まれていない地域にお住まいのご家庭でも、家庭教師を紹介できる場合もございますので、お気軽にお問い合わせください。

私たちジャニアスは、どんなに効果がある勉強法でもお子さんに合わない・
続けることができなければ「意味がない」と考えています。

塾や家庭教師選びにご苦労されているご家庭も多いと思いますが、ジャニアスの体験授業は、「やる気のきっかけにしたい」「今の塾と比べてみたい」「今すぐは考えてないけど家庭教師がどんなモノかを見てみたい」などのような、気軽な気持ちで受けていただけたらと思います。
もちろん、体験を受けたからといって、無理に入会を勧めるようなことは一切ありませんので、安心してくださいね(^^)











































