
数学が“一気に”パワーアップ!
“中2数学”の学習ポイント

中1の数学はいかがでしたか?
数学は思いっきり積み上げの教科です。
特に中1の「正負の数」「文字式」「方程式」の一連は中学数学の“基礎土台”になるところですので、少しでもニガテがあれば絶対に戻り学習をしてください。
「中1の時は何となく出来てたのに…」
「中2になって急に点数が下がった…」
そんなお子さんは、中1のところであやふやな部分があるかもしれません。
今すぐ中1数学の学習ポイントをチェックしてみて下さい!
中2ではこんなことを学習します。
このページでは中2の数学で押さえておきたい「式の計算」「連立方程式」「一次関数」の基礎ポイントをご紹介させていただきます。
こんなページも見られています!
>>中学2年生の教科別学習ポイント

2021年4月から中学校の教科書が全面的に改訂され、新しい学習指導要領による授業が開始されました。「数学」は、全ての学年に「データの活用」が追加され、これまで以上にグラフや資料から必要なことを”読み取る力”が重視されています。
もっと詳しく知りたい!
>>2021年からの中学数学はデータだらけ!?

計算がパワーアップ!
式の計算
中1の“正負の数と文字式”が、中2は“式の計算”となってパワーアップ!
新しい用語も出てくるので、1つ1つ確実に理解していきましょう!
★式の計算★
① 単項式と多項式
「単項式」 とは…?
数や文字のかけ算だけで出来ている式を「単項式」っていいます。
例えばこんなヤツ
\(-5x\)、\(ab\)、\(2x^2y\)、\(-0.8a\)

\(-5x=-5\)\(\times\)\(x\)
\(ab=a\)\(\times\)\(b\)
\(2x^2y=2\)\(\times\)\(x\)\(\times\)\(x\)\(\times\)\(y\)
\(-0.8a=-0.8\)\(\times\)\(a\)
すべてかけ算だけで作られていますよね。
また、1つの数字だけ、1つの文字だけも単項式です。
だからこんなのも単項式ですよ。
\(-12\)、\(a\)、\(y\)、\(8\)
「多項式」 とは…?
単項式が2つ以上あって、加法(たし算)で表されている式を「多項式」っていいます。
例えばこんなヤツ
\(3x+4y\)、\(2a+3\)、\(-5+6x\)
\(2x+y+4\)
単項式がたし算で結ばれていますよね!
ちなみにこんなのも多項式です。
\(-5a-7\)、\(x-6y\)、\(3x^2-2y\)
「たし算じゃなくてひき算じゃん!」
って思う人もいるかもしれませんが、これらも加法(たし算)の式なんですよ。
「\(-5a-7\)」はこうすることが出来ます。
\(-5a\)\(+\)\((-7)\)
「\(x-6y\)」はこう出来ます。
\(x\)\(+\)\((-6y)\)
「\(3x^2-2y\)」はこう出来ます。
\(3x^2\)\(+\)\((-2y)\)
たし算で結ばれましたよね!
だからひき算で結ばれている式もたし算に変えられるので多項式なんです。
このように、単項式はかけ算のみの式(文字だけ、数字だけも単項式)、多項式は単項式をたし算で結ぶ式ということを覚えておきましょう。
では問題です。
次の式が単項式か多項式か答えなさい。
問題
① \(5a\)
② \(-3ab\)
③ \(2x-1\)
④ \(-5a+2b\)
答え
① 単項式
② 単項式
③ 多項式
④ 多項式
単項式か多項式かを答えさせる問題は、中2初めの中間テストで必ず出ます!
ちゃんと理解していれば確実に取れるところなので、絶対に落とさないようにしていきましょう。
★式の計算★
② 次数
「次数」(じすう) とは…?
単項式でかけあわされている文字の個数を「次数」といいます。
例えば、”\(xy\)”の次数はいくつでしょうか?
”\(xy\)”は、”\(x\)\(\times\)\(y\)”ですので、2つの文字がかけられていますよね。
だから、”\(xy\)”の次数は2ということになります。
では、”\(-2a^2b\)”の次数を考えます。
”\(-2a^2b\)”は、”\(-2\)\(\times\)\(a\)\(\times\)\(a\)\(\times\)\(b\)”ですね。文字は何個あるでしょうか?
\(a\)と\(a\)と\(b\)の3個ですよね。
なので、”\(-2a^2b\)”の次数は3になります。
※数字(係数)の”\(-2\)”はカウントしないので要注意!
では問題です。
次の単項式の次数を答えなさい。
問題
① \(-5a\)
② \(3ab^2\)
③ \(x^2y\)
④ \(-3a^3b^2\)
答え
① 次数は \(1\)
② 次数は \(3\)
③ 次数は \(3\)
④ 次数は \(5\)
多項式の次数
次は多項式の次数です。
多項式っていうのは単項式をたし算で結ばれた式のことでしたよね。
では、\(3x+2y^3\) の次数を考えてみましょう。
まずは \(3x\) と \(2y^3\) のそれぞれの単項式の次数を求めます。
\(3x\) の次数は \(1\) です。
\(2y^3\) の次数は \(3\) です。
多項式ではその中に含まれる項の中で一番大きい次数がその多項式の次数になります。
\(3x+2y^3\) では、次数が \(1\)「\(3x\)」 と次数が \(3\)「\(2y^3\)」 なので、一番大きい次数は \(3\) ですね。
つまり、\(3x+2y^3\) の次数は \(3\) ということになります。
では、\(x^4+2y^2-ab^4\) の次数はどうでしょう?
それぞれの単項式で考えると…
\(x^4\) の次数は \(4\)
\(2y^2\) の次数は \(2\)
\(-ab^4\) の次数は \(5\)
この中で一番大きい次数は「\(-ab^4\)」の \(5\) ですね
ですので、\(x^4+2y^2-ab^4\) の次数は \(5\) になります。
また、次数が〇の式のことを「〇次式」といいます。
次数が \(2\) の式は「\(2\) 次式」ですね。
先ほどの例だと…
\(3x+2y^3\) は「\(3\) 次式」
\(x^4+2y^2-ab^4\) は「\(5\) 次式」
では問題です。
次の式は何次式か答えなさい。
問題
① \(2x+1\)
② \(-x^3\)
③ \(a-b^2\)
④ \(3a-x^2y^4\)
答え
① \(1\) 次式
② \(3\) 次式
③ \(2\) 次式
④ \(6\) 次式
何次式かを求められる問題も定期テストでよく出るので、よく練習しておきましょう!
★式の計算★
③ 同類項
「同類項」(どうるいこう) とは…?
「\(2x\) と \(5x\)」「\(3a\) と \(4a\) 」など、文字の部分が同じ項を同類項っていいます。
こんなのも同類項
\(x^2\) と \(-5x^2\)
文字の部分が全く同じ \(x^2\) ですね。
\(2ab\) と \(-4ab\)
文字の部分が同じ \(ab\) ですね。
これは同類項ではありません。
\(3a\) と \(-2a^2\)
同じ \(a\) じゃん!って思うかもしれませんが、\(a\) の次数が違いますよね。
\(5x^2\) と \(2x^3\)
これも同じ \(x\) でも2乗と3乗で異なります。
このように文字が同じでも、次数が異なると同類項ではないので要注意!
「同類項」をまとめる
同類項は計算してまとめることができます。
例えば \(3a+2a\) は文字の部分 \(a\) が同じなので同類項ですね。
同類項どうしは計算ができるので、
\(3a+2a=\)\(5a\) となります。
これらは計算してまとめることが出来ます。
\(-3x^2+5x^2=\)\(2x^2\)
\(2ab-5ab=\)\(-3ab\)
\(x+3x-6x=\)\(-2x\)
これらは同類項どうしではないのでこれ以上は計算できません。
\(-x+2y\)
\(2x^2+8x\)
\(3ab+4a\)
\(3x-5\)
では同類項をまとめる練習をしてみましょう!
問題①
\(2a+3b-5b+4a\)
まず同類項どうしで順番を並び替えます。
\(2a+4a+3b-5b\)
同類項を計算します。
\(6a-2b\)
同類項をまとめることができました。
これ以上は同類項がないので計算できませんね。
答え. \(6a-2b\)
問題②
\(-5x^2+2x-3x^2+5x+6\)
同類項どうしに順番を変えます。
\(-5x^2-3x^2+2x+5x+6\)
同類項を計算します。
\(-8x^2+7x+6\)
同類項をまとめることができました。
※\(-8x^2\)と\(+7x\) は同類項ではないので要注意!
答え. \(-8x^2+7x+6\)
★式の計算★
④ 式の加法と減法
同類項をまとめる計算はいかがでしたか?
ここまでのやり方が理解出来ていれば、次の計算も大丈夫ですよ!
「式の加法」 式と式をたします。
問題.
次の2つの式をたしなさい。
\(5x+2y\)、\(3x+y\)
2つの式をたす場合はそれぞれの式にカッコをつけて+でつないで計算します。
\((\)\(5x+2y\)\()\) \(+\) \((\)\(3x+y\)\()\)
カッコを外し、同類項どうしに並び替えて計算します。
\((5x+2y)+(3x+y)\)
\(=5x+2y+3x+y\)
\(=5x+3x+2y+y\)
\(=8x+3y\)
答え. \(8x+3y\)
問題.
次の2つの式をたしなさい。
\(-2a+3b\)、\(-5a-4b\)
\((-2a+3b)+(-5a-4b)\)
\(=-2a+3b-5a-4b\)
\(=-2a-5a+3b-4b\)
\(=-7a-b\)
答え. \(-7a-b\)
「式の減法」 式から式を引きます。
問題.
左の式から右の式を引きなさい。
\(6x+4y\)、\(2x+3y\)
2つの式を引く場合はそれぞれの式にカッコをつけて-でつないで計算します。
\((\)\(6x+4y\)\()\) \(-\) \((\)\(2x+3y\)\()\)
カッコを外し、同類項どうしに並び替えて計算します。
\((6x+4y)-(2x+3y)\)
\(=6x+4y-2x-3y\)
\(=6x-2x+4y-3y\)
\(=4x+y\)
答え. \(4x+y\)
問題.
左の式から右の式を引きなさい。
\(-2a-3b+2\)、\(5a+6b+5\)
\((-2a-3b+2)-(5a+6b+5)\)
\(=-2a-3b+2-5a-6b-5\)
\(=-2a-5a-3b-6b+2-5\)
\(=-7a-9b-3\)
答え. \(-7a-9b-3\)
また、多項式の加法・減法では、同類項が上下にそろうように並べて計算することもできます。
\((4x+2y)+(-2x+3y)\)
\(4x+2y\)
\(\underline{+)-2x+3y}\)
\(2x+5y\)
答え. \(2x+5y\)
\((3a-5b)-(-2a+3b)\)
\(3a-5b\)
\(\underline{-)-2a+3b}\)
\(5a-8b\)
答え. \(5a-8b\)
\((2x^2-5x+3)+(-3x^2+2x-5)\)
\(2x^2-5x+3\)
\(\underline{+)-3x^2+2x-5}\)
\(-x^2-3x-2\)
答え. \(-x^2-3x-2\)
★式の計算★
④ 単項式の乗法と除法
単項式の乗法(かけ算)
数字は数字どうしで掛けて、文字は文字どうしで掛けていきます。
\(2a\times4b\)
\(=2×a×4×b\)
\(=2×4×a×b\)
\(=6ab\)
\(-3x×6y\)
\(=-3×x×6×y\)
\(=-3×6×x×y\)
\(=-18xy\)
\(-2x×3x\)
\(=-2×x×3×x\)
\(=-2×3×x×x\)
\(=-6x^2\)
\(-x×(-4xy)\)
\(=-x×(-4)×x×y\)
\(=-4×(-x)×x×y\)
\(=4x^2y\)
\((-5y)^2×2xy\)
\(=-5×y×(-5)×y×2×x×y\)
\(=-5×(-5)×2×x×y×y×y\)
\(=100xy^3\)
慣れると途中式は考えずに頭の中で計算できるようになるので、たくさん練習しましょうね!
単項式の除法(わり算)
分数にして約分するのがわかりやすいです。
\(8x^2÷2x\)
\(=\)\(\frac{8x^2}{2x}\)
\(=4x\)
\(-9xy^3÷3y\)
\(=\)\(\frac{-9xy^3}{3y}\)
\(=-3xy^2\)
\(12ab^5÷4b^3\)
\(=\)\(\frac{12ab^5}{4b^3}\)
\(=3ab^2\)
分数が含まれる場合は、割る数を逆数にしてかけましょう。
\(-3x^2÷\)\(\frac{6x}{2}\)
\(=-3x^2×\)\(\frac{2}{6x}\)(←割る数を逆数にしてかける)
\(=-x\)
\(\frac{2x}{3}\)÷\(\frac{2}{3x}\)
\(=\)\(\frac{2x}{3}\)×\(\frac{3x}{2}\)(←割る数を逆数にしてかける)
\(=x^2\)
この辺りでわからなくなっている子は、中1の文字式があやふやかもしれないので早めに復習してください。
中1数学の学習ポイントでも紹介していますので見てくださいね!
超本格的な数学に
連立方程式
中1の数学では“方程式”(一元一次方程式)をやりましたよね。“等式の性質”とか“移項”とかちゃんと覚えていますか?
中2の数学では“連立方程式”(二元一次方程式)ってやつを学習していきます。
ハッキリ言って、“方程式”がわからないと“連立方程式”は絶対にわかりません。
この辺りの関連性はとっても高いので、何度も言いますが中1の基礎は絶対に押さえておいてくださいね!!
中1で習った方程式はこんなのでした。
\(2x+1=7\)
移項して「\(x=\)〇〇」の形にしましたよね。
\(2x+1=7\)
\(2x=7-1\)
\(2x=6\)
\(x=3\)
方程式では求める値(方程式の解)が1つでした。
連立方程式では求める値が2つあるので、計算の手順や方法が増えていくのが厄介なんです…。
連立方程式は、定期テストはもちろん、高校入試でも必ず出題されるので、絶対に取りこぼしのないようにしていきましょう!
連立方程式ってこんなのです。
\(2x+y=3\)
\(x-3y=-1\)
中1の方程式と違って、\(y\) がありますね。
ここでは「\(x=\)〇〇」と「\(y=\)〇〇」の2つの値を求めていきます。
連立方程式には“加減法”と“代入法”の2つの解き方があるので、それぞれを解説していきます。
★連立方程式の解き方★
① 加減法
加減法は、2つの式をそれぞれ足したり引いたりして連立方程式の解を導く方法です。
では具体的にやってみましょう!
【問題1】
次の連立方程式を解きなさい
\(2x+4y=6\)
\(2x-8y=-18\)
<手順1>
\(x\) と \(y\) の係数の絶対値に注目
2つの式のそれぞれ \(x\) の係数と \(y\) の係数の絶対値に注目します。
\(x\) の係数の絶対値は①の式も②の式も「\(2\)」で同じすね。
\(2\)\(x+4y=6\) ・・・①
\(2\)\(x-8y=-18\) ・・・②
\(y\) の係数の絶対値は①の式は「\(4\)」で②の式は「\(8\)」です。
\(2x+\)\(4\)\(y=6\) ・・・①
\(2x-\)\(8\)\(y=-18\) ・・・②
\(x\) か \(y\) のどちらか1つの係数の絶対値が同じなら、上の式と下の式を足すか引くかをすれば \(x\) か \(y\) のどちらかの項が消えます!
<手順2>
2つ式を足すか引くかして \(x\) か \(y\) の項を消す
係数とその符号に注目!
符号が同じなら引く
符号が違うなら足す
この連立方程式の場合は、xの係数がそれぞれ「2」で符号も「+」で同じなので、①の式から②の式を引くとxの項が消えるんです。
※「2」というのは「+2」のことなので符号も同じ「+」ですね。
では①の式から②の式を引いてみます。
\(2x+4y=6\)
\(\underline{-)2x-8y=-18}\)
\(12y=24\)
\(x\) の項が消えたので、\(y\) の値が求められます。
\(12y=24\)
\(y=2\)
<手順3>
①か②の好きなほうの \(y\) に \(2\) を代入して \(x\) の値を求める。
では①の式の \(y\) に \(2\) を代入してみましょう。
\(2x+4\)\(y\)\(=6\)
↑\(y\) に \(2\) を代入
\(2x+4\)\(×2\)\(=6\)
\(2x+8=6\)
\(2x=6-8\)
\(2x=-2\)
\(x=-1\)
<手順4>
答えを書きます。
\(x=-1,y=2\)
こんな書き方でもOK!
\((x,y)=(-1,2)\)
【問題1】では \(x\) の係数がそれぞれ \(2\) で同じでした。
では次の問題はどうでしょう?
【問題2】
次の連立方程式を解きなさい
\(2x-3y=13\)
\(5x+2y=4\)
2つの式の \(x\) の係数と \(y\) の係数がそれぞれ違いますよね。 \(x\) の係数は \(2\) と \(5\) で、\(y\) の係数は \(-3\) と \(2\) です…。
このままだと、2つ式を足したり引いたりしても、\(x\) の項も \(y\) の項も消えません。
<手順①>
\(x\) か \(y\) の係数の絶対値をそろえる
ここでは \(x\) の係数をそろえてみます。
①の \(x\) の係数は \(2\) です。
②の \(x\) の係数は \(5\) です。
\(2\)\(x-3y=13\) ・・・①
\(5\)\(x+2y=4\) ・・・②
\(2\) と \(5\) の最小公倍数を求めて、係数の絶対値をそろえます。
\(2\) と \(5\) の最小公倍数は \(10\) ですね。
\(2\) を \(10\) にするために①の式に \(×5\) をします。
\(5\) を \(10\) にするために②の式に \(×2\) をします。
\(2x-3y=13\) ⇒ \(×5\) ・・・①
\(5x+2y=4\) ⇒ \(×2\) ・・・②
\(10\)\(x-15y=65\) ・・・①
\(10\)\(x+4y=8\) ・・・②
これで \(x\) の係数の絶対値が \(10\) でそろいました。
<手順②>
①から②を引いて \(x\) の項を消します。
※①も \(10\) も②の \(10\) も同じ符号どうし\((+)\)なので引きます。
\(10x-15y=65\) ・・・①
\(\underline{-)10x-4y=8}\) ・・・②
\(-19y=57\)
\(x\) の項が消えたので、\(y\) の値が求められます。
\(-19y=57\)
\(y=-3\)
<手順③>
①か②の好きなほうの \(y\) に \(-3\) を代入して \(x\) の解を求める。
では②の式の \(y\) に \(-3\) を代入してみましょう。
\(5x+2\)\(y\)\(=4\)
↑\(y\) に \(-3\) を代入
\(5x+2×\)\((-3)\)\(=4\)
\(5x-6=4\)
\(5x=4+6\)
\(5x=10\)
\(x=2\)
<手順④>
答えを書きます。
\(x=2,y=-3\)
こんな書き方でもOK!
\((x,y)=(2,-3)\)
【問題3】
次の連立方程式を解きなさい
\(-4x+3y=20\)
\(5x-4y=-26\)
この問題も係数がそれぞれ異なりますね。
<手順1>
\(x\) か \(y\) の係数の絶対値をそろえる
では \(y\) の係数の絶対値をそろえてみましょう。
\(-4x+\)\(3\)\(y=20\) ・・・①
\(5x-\)\(4\)\(y=-26\) ・・・②
①の\(+3\) の絶対値は \(3\)、②の \(-4\) の絶対値は \(4\) です。
\(3\) と \(4\) の最小公倍数は \(12\) ですね。
\(3\) を \(12\) にするために①の式に \(×4\) をします。
\(4\) を \(12\) にするために②の式に \(×3\) をします。
\(-4x+3y=20\) ⇒ \(×4\) ・・・①
\(5x-4y=-26\) ⇒ \(×3\) ・・・②
\(-16x+\)\(12\)\(y=80\) ・・・①
\(15x-\)\(12\)\(y=-78\) ・・・②
これで \(y\) の係数の絶対値が \(12\) でそろいました。
<手順2>
\(y\) の係数は \(+12\) と \(-12\) で符号が異なるので、①と②の式をたして \(y\) の項を消します。
\(-16x+12y=80\) ・・・①
\(\underline{+) 15x-12y=-78}\) ・・・②
\(-x=2\)
\(-x=2\)
\(x=-2\)
<手順3>
①か②の好きなほうの \(x\) に \(-2\) を代入して \(y\) の値を求める。
では①の式の \(x\) に \(-2\) を代入してみましょう。
\(-4\)\(x\)\(+3y=20\)
↑\(x\) に \(-2\) を代入
\(-4×(-2)+3y=20\)
\(8+3y=20\)
\(3y=20-8\)
\(3y=12\)
\(y=4\)
<手順4>
答えを書きます。
\(x=-2\)、\(y=4\)
こんな書き方でもOK!
\((x,y)=(-2,4)\)
★連立方程式の解き方★
② 代入法
代入法は一方の式を他方の式に代入して、一元一次方程式の形で解く方法です。
どちらかの式に「 \(y=\) 〇〇」「 \(x=\) 〇〇」の形があれば代入法で解く方が楽ですよ!
では具体的にやってみましょう!
【問題1】
次の連立方程式を解きなさい
\(y=3x-1\)
\(2x+y=9\)
①の式が「 \(y=\) 〇〇」の形ですので代入法で解いてみます。
\(y=\) \(3x-1\)・・・①
\(2x+y=9\)・・・②
<手順1>
「\(y=\)」か「\(x=\)」のあとの式をカッコでくくって、もう一方の式に代入する。
①の式が「\(y=\)」の形ですね。
では \(3x-1\) をカッコでくくって、②の式の \(y\) の部分に代入します。
\(y=\)\((\)\(3x-1\)\()\)
\(2x+\)\(y\)\(=9\)
↑\(y\) に \((3x-1)\) を代入
\(2x+(3x-1)=9\)
↑代入したらこうなりました。
<手順2>
一元一次方程式を解く
\(2x+(3x-1)=9\)
\(2x+3x-1=9\)
\(5x-1=9\)
\(5x=9+1\)
\(5x=10\)
\(x=2\)
<手順3>
もう一方の式の \(x\) に「\(2\)」を代入して \(y\) の値を出す。
\(y\) の値を求めるので、「\(y=3x-1\)」に代入しましょう。
\(y=3\)\(x\)\(-1\)
↑\(x\)に「\(2\)」を代入します。
\(y=3\)\(×2\)\(-1\)
\(y=6-1\)
\(y=5\)
<手順4>
答えを書きます。
\(x=2\)、\(y=5\)
こんな書き方でもOK!
\((x,y)=(2,5)\)
【問題2】
次の連立方程式を解きなさい
\(x=4y-2\)
\(3x-5y=-20\)
①の式が「 \(x=\) 〇〇」の形ですので代入法で解いてみます。
\(x=\) \(4y-2\) ・・・①
\(3x-5y=-20\)・・・②
<手順1>
①の式が「\(x=\)」の形ですね。
では \(4y-2\) をカッコでくくって、②の式の \(x\) に代入します。
\(x=\)\((\)\(4y-2\)\()\)
\(3\)\(x\)\(-5y=-20\)
↑\(x\) に \((4y-2)\) を代入
\(3(4y-2)-5y=-20\)
<手順2>
一元一次方程式を解く
\(3(4y-2)-5y=-20\)
\(12y-6-5y=-20\)
\(7y-6=-20\)
\(7y=-20+6\)
\(7y=-14\)
\(y=-2\)
<手順3>
もう一方の式の \(y\) に「\(-2\)」を代入して \(x\) の値を出す。
\(x\) の値を求めるので、「\(x=4y-2\)」に代入しましょう。
\(x=4\)\(y\) \(-2\)
↑\(y\) に「\(-2\)」を代入します。
\(x=4×(-2)-2\)
\(x=-8-2\)
\(x=-10\)
<手順4>
答えを書きます。
\(x=-10\)、\(y=-2\)
こんな書き方でもOK!
\((x,y)=(-10,-2)\)
【問題3】
次の連立方程式を解きなさい
\(4x+y=-17\)
\(7x-3y=-6\)
この連立方程式は、どこにも「\(x=\)」「\(y=\)」の形がありませんね。
こういう場合は加減法のほうが解きやすいのですが、あえて代入法で解いてみます。
<手順1>
どちらかの式を「\(x=\)」「\(y=\)」の形に変える
では「\(4x+y=-17\)」の式を「\(y=\)」の形にしでみましょう。
\(4x+y=-17\)
↓\(y=\) の形にします
\(y=-4x-17\)
\(4x+y=-17\)
\(7x-3y=-6\)
↓
\(y=-4x-17\) ・・・①
\(7x-3y=-6\) ・・・②
<手順2>
①の「\(-4x-17\)」にカッコをつけて、②の \(y\) に代入します。
\(y=\) \((\)\(-4x-17\)\()\) ・・・①
\(7x-3\)\(y\) \(=-6\) ・・・②
↓
\(7x-3(-4x-17)=-6\)
<手順3>
一元一次方程式を解く
\(7x-3(-4x-17)=-6\)
\(7x+12x+51=-6\)
\(19x+51=-6\)
\(19x=-6-51\)
\(19x=-57\)
\(x=-3\)
<手順4>
①の「\(y=-4x-17\)」の \(x\) に「\(-3\)」を代入して \(y\) の値を出す。
\(y=-4\)\(×(-3)\)\(-17\)
\(y=12-17\)
\(y=-5\)
<手順5>
答えを書きます。
\(x=-3\)、\(y=-5\)
こんな書き方でもOK!
\((x,y)=(-3,-5)\)
いかがでしたか?
連立方程式は、「加減法」「代入法」のどちらの方法でも解けますが、式の形によって解きやすい方法で解く方が楽ですよ!
でも定期テストでは「加減法で解きなさい」「代入法で解きなさい」という指示をされることも多いので、どちらの方法でも解けるように練習していきましょう!
基本式とグラフを理解しよう
一次関数
ここからグラフに突入です!
グラフと言えば中1では“比例・反比例”でやりましたよね。
中2では“一次関数”となってパワーアップしちゃいます…。
“一次関数”って名前も難しそうですよね…。取っ付きにくい単元だと感じる中2生も多いですが、わかっちゃえば面白いので頑張っていきましょう!!
★一次関数★
① 一次関数の基本式
一次関数では「基本式」を覚えて理解することが絶対的に必要です。

一次関数の基本式
絶対暗記!!
\(y=ax+b\) を何度も書いて、何度もぶつぶつ言って、確実に覚えてください!!
定期テストや入試テストで一次関数の問題が出たら、すぐに問題用紙の余白に \(y=ax+b\) を書いて下さい!
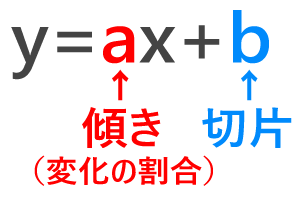
\(a\) と \(b\) を“定数”といって数字が入ります。( \(a\) は \(0\) 以外)
\(a\) の部分を“傾き”、\(b\) の部分を“切片”っていいます。
また、\(a\) の部分を“変化の割合”ともいいます。
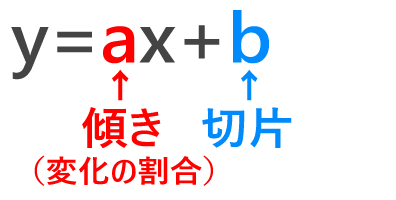
\(a\) と \(b\) を“定数”といって数字が入ります。
( \(a\) は \(0\) 以外)
\(a\) の部分を“傾き”、\(b\) の部分を“切片”っていいます。
また、\(a\) の部分を“変化の割合”ともいいます。
いくつか練習してみましょう!
傾きが \(2\)、切片が \(-3\) の一次関数の式を書きなさい
答え. \(y=2x-3\)
傾きが \(-1\)、切片が \(5\) の一次関数の式を書きなさい
答え. \(y=-x+5\)
変化の割合が \(3\)、切片が \(10\) の一次関数の式を書きなさい
答え. \(y=3x+10\)
一次関数 \(y=-5x-2\) の傾きと切片を言いなさい
答え. 傾き\(-5\)、切片\(-2\)
傾き、変化の割合は、\(y=\)\(a\)\(x+b\) の \(a\) に代入、
切片は、\(y=ax+\)\(b\) の \(b\) に代入するだけです。
★一次関数★
② 変化の割合について
変化の割合とは、\(x\) の増加量に対する \(y\) の増加量の割合です。
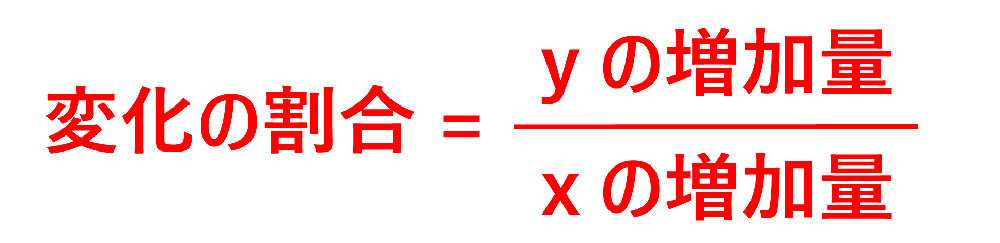
↑これも超大事!!絶対暗記!!
増加量とか割合とか…、ムズカシイと感じる子も多いと思います。
大事な所なので詳しく説明しますね。
増加量っていうのは「増えた分の量」です。
例えば「\(2\) から \(5\) に増えた」ということは、増加量は \(3\) になります。
※増加量は2つの数字の差(ひき算)なので「\(5-2\)」なので \(3\) だからです。
たとえば「\(-3\) から \(2\) に増えた」となったら増加量はいくつかわかりますか?
答えは \(5\) です。「\(2-(-3)\)」となるからです。
では、\(x\) が \(2\) から \(5\) に増えて、\(y\) が \(4\) から \(10\) に増えた時の変化の割合を求めてみましょう。
\(x\) の増加量 \(=5-2=\) \(3\)
\(y\) の増加量 \(=10-4=\) \(6\)
変化の割合は \(\frac{yの増加量}{xの増加量}\) なので \(\frac{6}{3}\)\(=2\)
つまり・・・
この場合の変化の割合は「\(2\)」です。
「変化の割合」は、グラフを書くときや直線の式を求めるときなどにとっても大事な考え方なので、理解を深めていきましょう!
★一次関数★
③ 傾きについて
傾きとは、一次関数の直線のグラフの傾き具合のことです。
たとえば、グラフの横方向( \(x\) 軸)に \(2\) 進んだときに、縦方向( \(y\) 軸)に \(6\) 進んだ時の傾きを考えてみましょう。
傾きは先ほどの変化の割合と同じ考え方で、\(\frac{y方向に進んだ量}{x方向に進んだ量}\) で表すので、上記の場合は \(\frac{6}{2}\) なので傾きは「\(3\)」になります。
一次関数においては、“傾き”と“変化の割合”は同じであると覚えて大丈夫です。
傾きは一次関数のグラフで「傾き具合」を表して、変化の割合は「\(x\) の増加量に対して \(y\) の増加量の割合」を表しています。
深く考えれば意味が異なりますが、一次関数においては、傾きと変化の割合は同じで、\(y=ax+b\) の \(a\) の部分であると覚えておきましょう!
★一次関数★
④ 直線の式→グラフ
一次関数の直線のグラフを書く問題は定期テストで必ず出ます!
確実に書けるようにしましょうね!
グラフってこんなやつ!
横の軸が \(x\) で、縦の軸が \(y\)、真ん中の原点がOです。
※OはアルファベットのO(オウ)です。数字の \(0\)(ゼロ)ではありません。
練習してみましょう!
\(y=2x+1\)
のグラフを書いてみます。
傾きと切片に注目!!
傾きは「2」、切片は「+1」ですね!
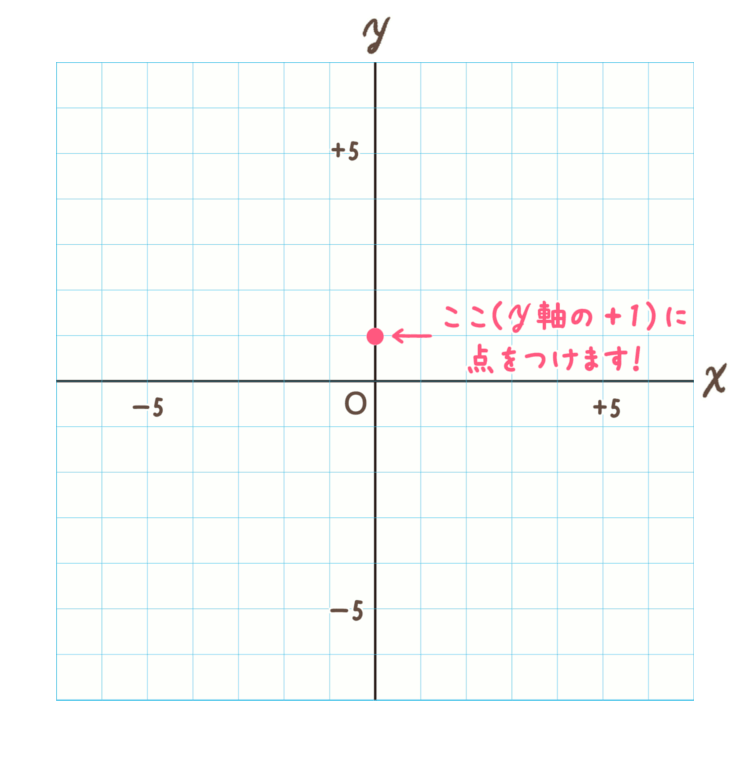
<手順1>
まずは切片の \(+1\)
\(y=2x+1\) の切片は \(+1\) ですね。
切片は \(y\) 軸に接しますので、 \(y\) 軸の \(+1\) に点をつけます。
<手順2>
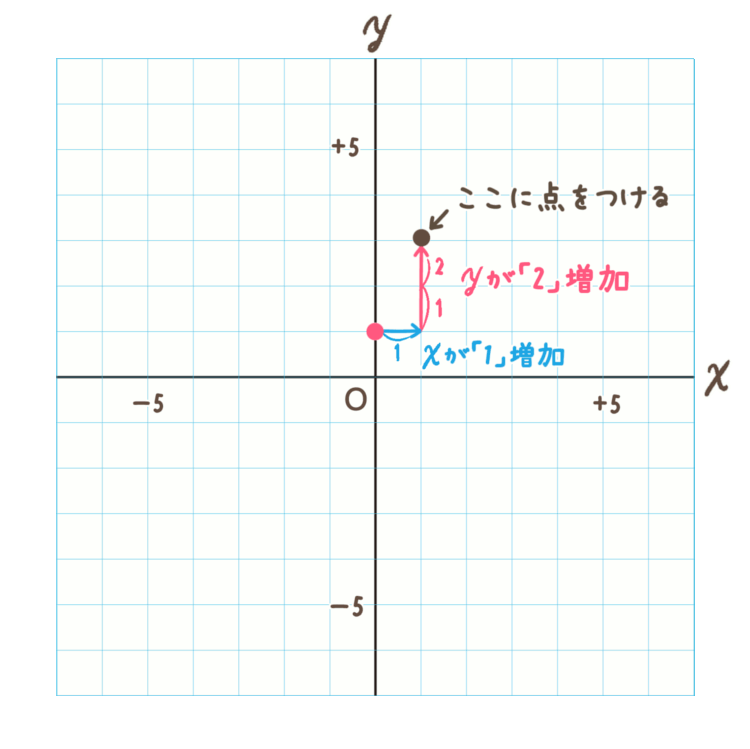
次は傾きの \(2\)
傾きに注目!
\(y=2x+1\) の傾きは \(2\) ですね。
傾きというのは変化の割合と同じなので、
\(\frac{yの増加量}{xの増加量}\) です!
傾き「\(2\)」を分数で表すと \(\frac{2}{1}\) です。
つまり、傾きが \(\frac{2}{1}\) ということは、\(x\) が \(1\) 増加した時に \(y\) が \(2\) 増加するということです。
では、先ほど切片( \(y\) 軸)に点をつけた位置から、\(x\) を \(1\) 増加させ、\(y\) を \(2\) 増加させてみましょう。
※ \(x\) は横の軸、\(y\) は縦の軸です。
<手順3>
2点を直線で結びます。
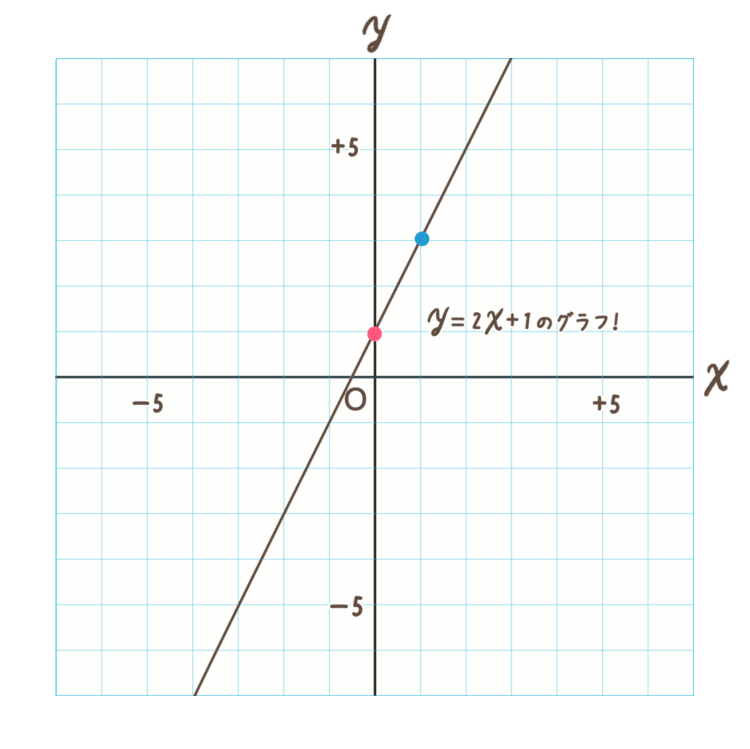
\(y=2x+1\) の直線のグラフが書けました!
次に、
\(y=-\)\(\frac{1}{3}\)\(x-2\)
のグラフを書いてみます。
傾きは \(-\)\(\frac{1}{3}\)、切片は \(-2\) です。
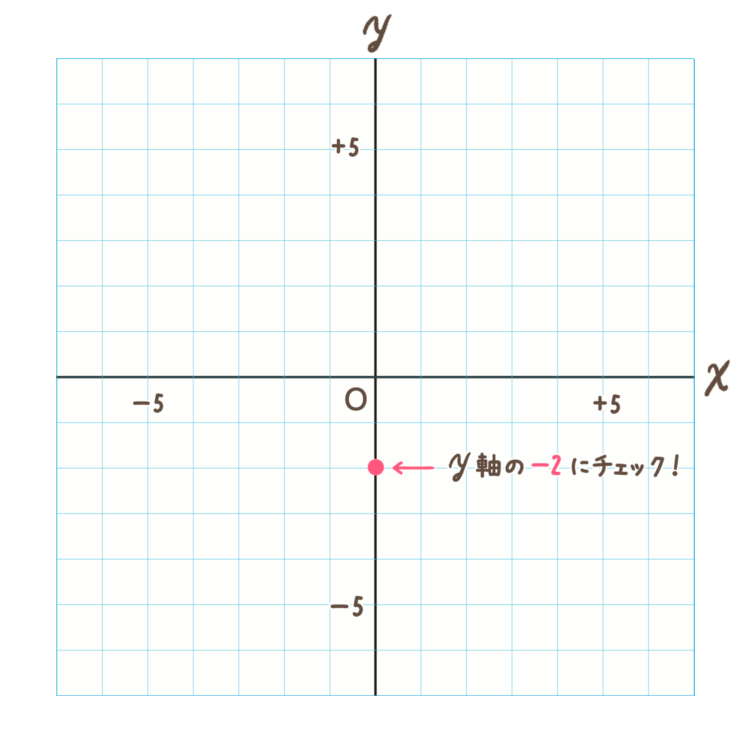
<手順1>
まずは切片の \(-2\)
切片は \(y\) 軸に接しますので、 \(y\) 軸の \(-2\) に点をつけます。
<手順2>
次は傾きの \(-\)\(\frac{1}{3}\)
傾きというのは変化の割合と同じなので、
\(\frac{yの増加量}{xの増加量}\) です!
つまり、傾きが \(-\)\(\frac{1}{3}\) ということは、\(x\) が \(3\) 増加した時に \(y\) が \(-1\) 増加するということです。
(注意)「\(-1\) 増加」ということは「\(1\) 減少」と同じ意味です。
さきほどチェックした \(y\) 軸の点から、\(x\) の方向(横方向)に \(3\) 増加させ、\(y\) の方向(縦方向)に \(-1\) 増加させます。
※ \(-1\) 増加ということは、\(1\) 減少させるということなので、下向きに1進めます。
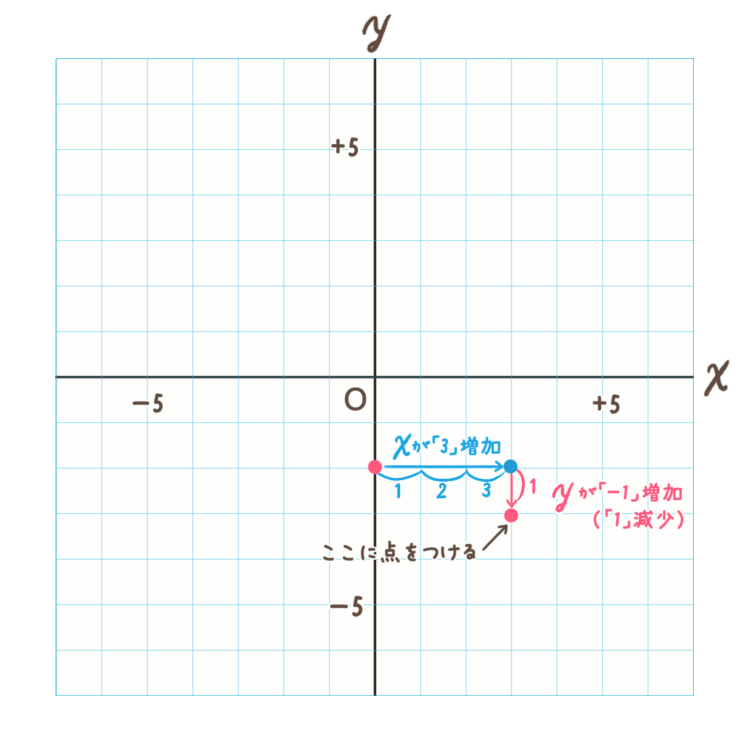
<手順3>
2点を直線で結びます。
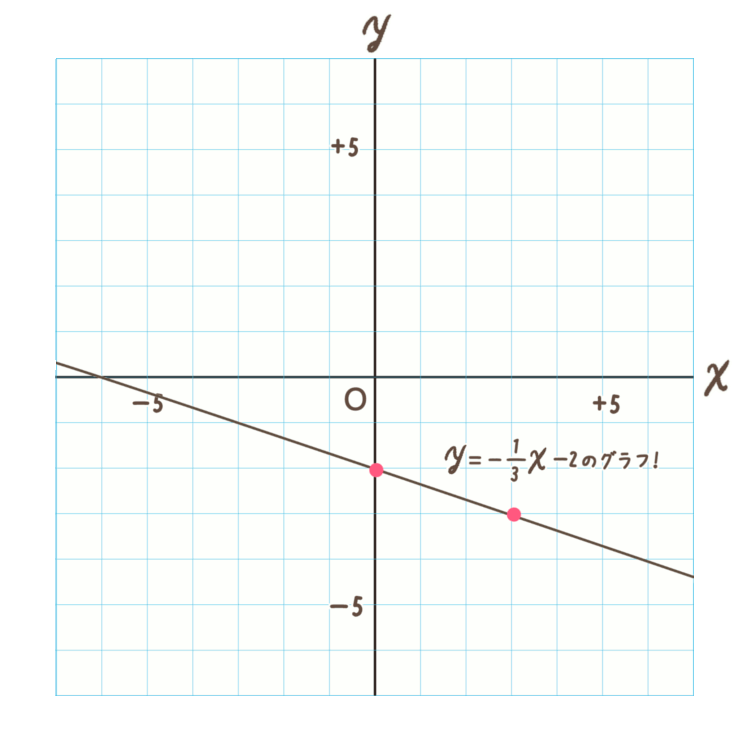
\(y=-\)\(\frac{1}{3}\)\(x-2\) の直線のグラフが書けました!
ではいくつか練習してみましょう!
次の直線の式をグラフに書きなさい。
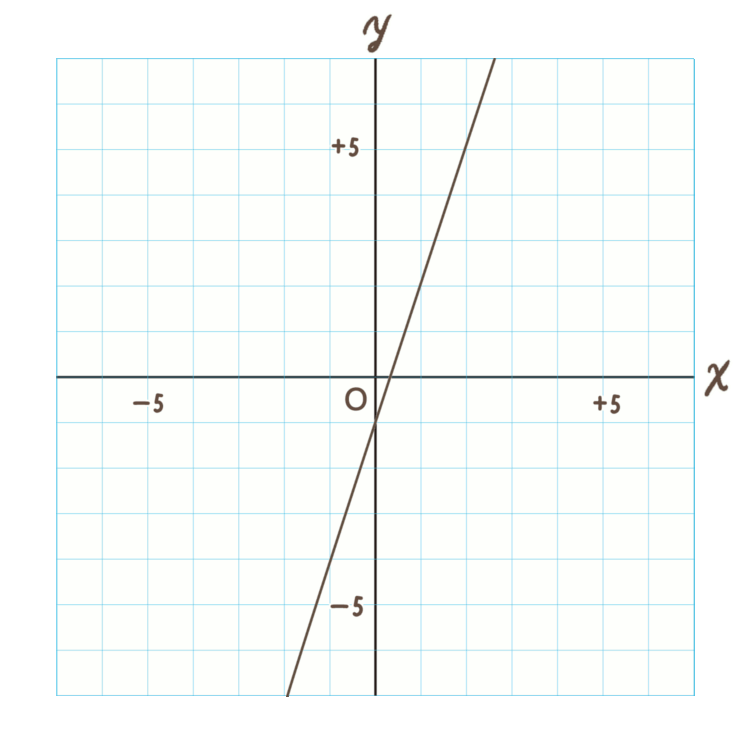
(1)\(y=3x-1\)
(2)\(y=-\)\(\frac{1}{4}\)\(x+2\)
(3)\(y=-2x+3\)
答え
(1)\(y=3x-1\)
(2)\(y=-\)\(\frac{1}{4}\)\(x+2\)
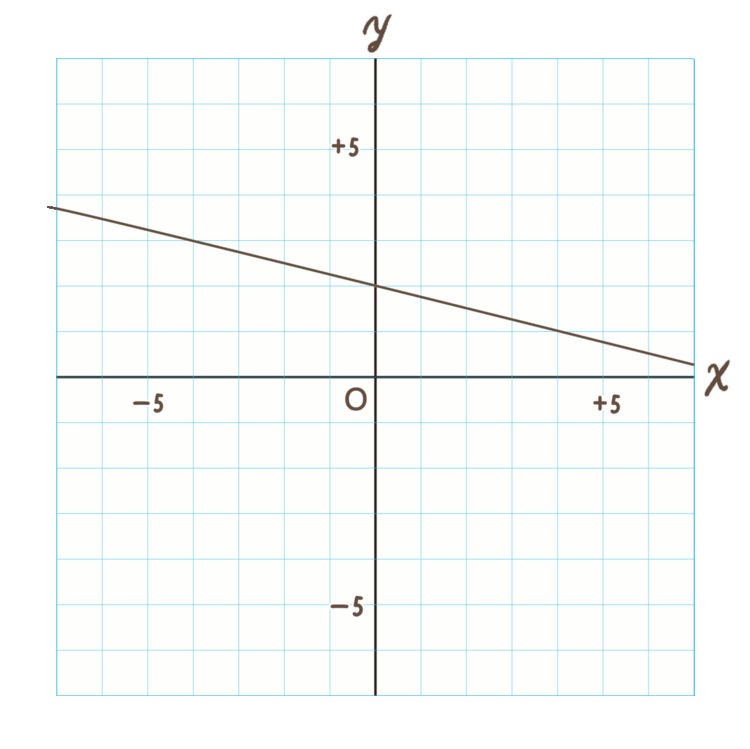
(3)\(y=-2x+3\)
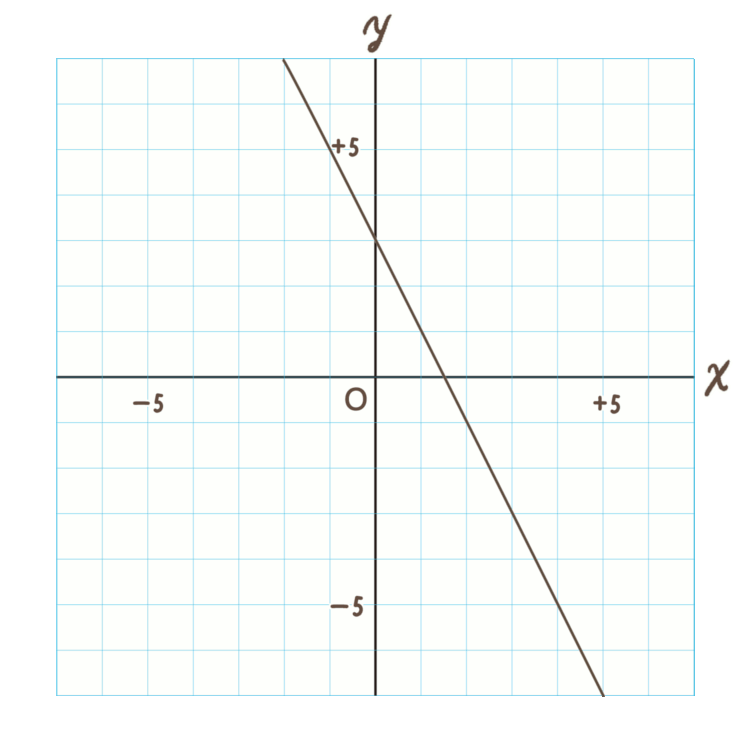
★一次関数★
⑤ グラフ→直線の式
先ほどは直線の式からグラフを書きました。
今度はその逆で、グラフから直線の式を読み解いていきます。
では、直線の式を求める手順を紹介します。
問題.
このグラフの直線の式を求めなさい。
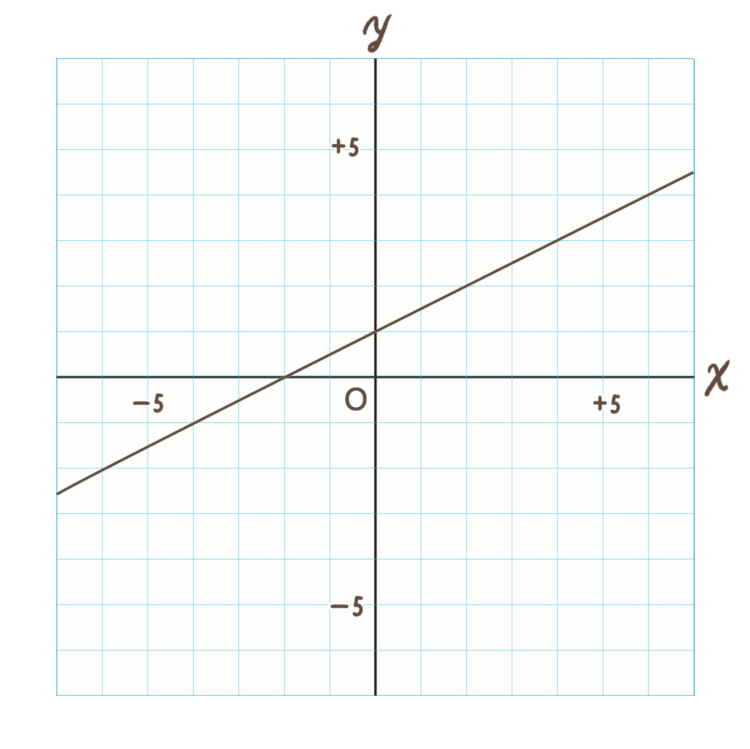
一次関数の直線の式を求めるということは、\(a\)(傾き)と \(b\)(切片)がわかれば、基本式「\(y=ax+b\)」にあてはめるだけですね。
<手順1>
切片 \(b\) を求める
切片は \(y\) 軸と交差しているところです。
この直線で \(y\) 軸に交差しているところは「\(+1\)」ですね。
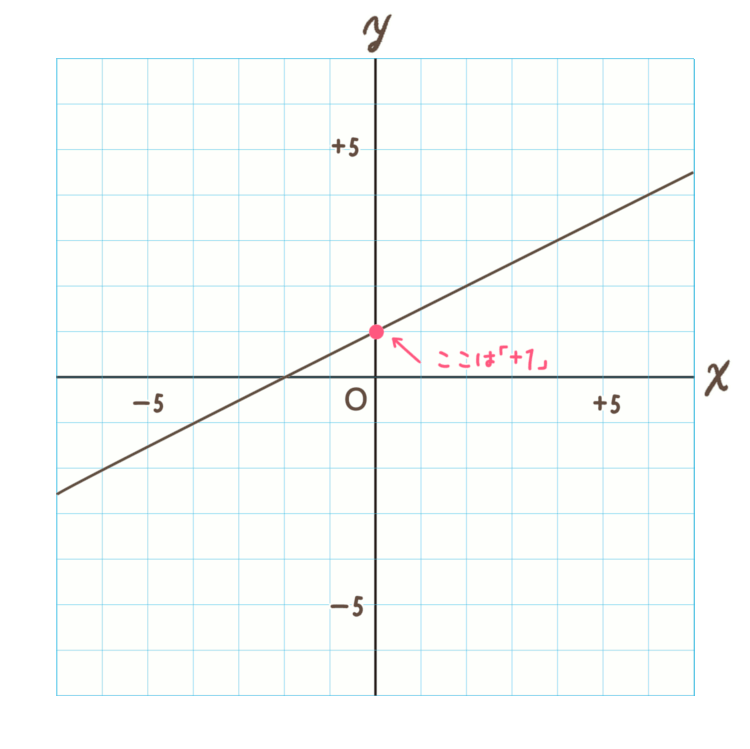
これで切片 \(b\) は「 \(+1\) 」ということがわかりました。
<手順2>
傾き \(a\) を求める
切片は簡単でしたが、傾きは少し面倒です…。
グラフのマス目で、縦の線と横の線で、直線と交差している2か所に点をつけます。
1か所は先ほど付けた \(y\) 軸の「+1」のところで大丈夫です。
もう1か所は、下のグラフで青いところに点をつけました。
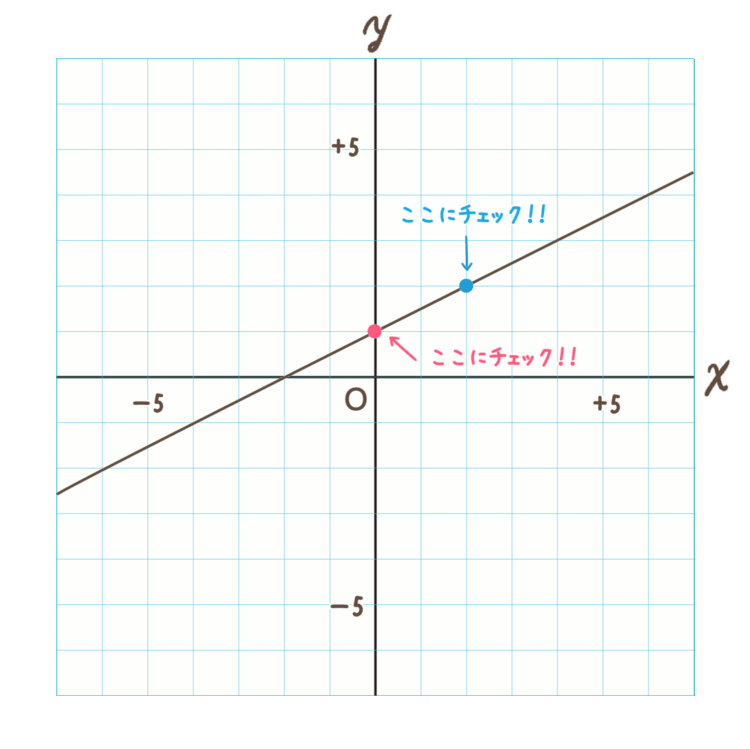
2点にチェックをつけたら、変化の割合を調べます。
変化の割合は、\(\frac{yの増加量}{xの増加量}\)です。
下のグラフを見てもらうと、①の点から②の点まで \(x\) が \(2\) 増加、\(y\) が \(1\) 増加していることがわかりますね。
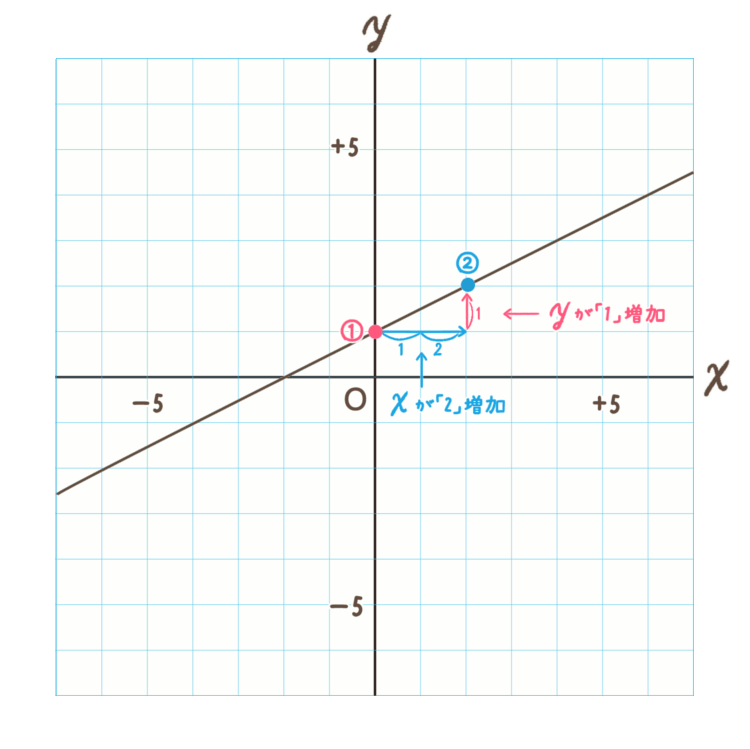
\(\frac{yの増加量=1}{xの増加量=2}\)なので、変化の割合は \(\frac{1}{2}\) です。
一次関数においては、”変化の割合=傾き”なので、傾き \(a\) は \(\frac{1}{2}\) であるということがわかりました。
<手順3>
基本式 \(y=ax+b\) に求めた \(a\) の値と \(b\) の値を入れます。
\(a\)(傾き)は \(\frac{1}{2}\) でした。
\(b\)(切片)は \(+1\) でした。
答え. \(y=\)\(\frac{1}{2}\)\(x+1\)
ではこのグラフも直線の式を求めてみましょう。
問題.
このグラフの直線の式を求めなさい。
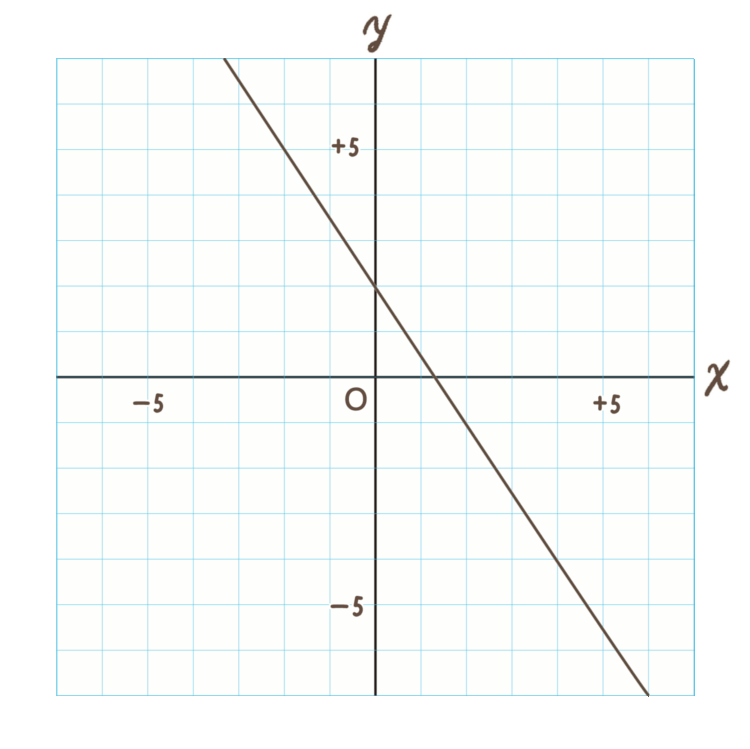
<手順1>
まずは切片を求めます。
切片 \(b\) は \(y\) 軸に接しているところなので、「 \(+2\) 」ですね。
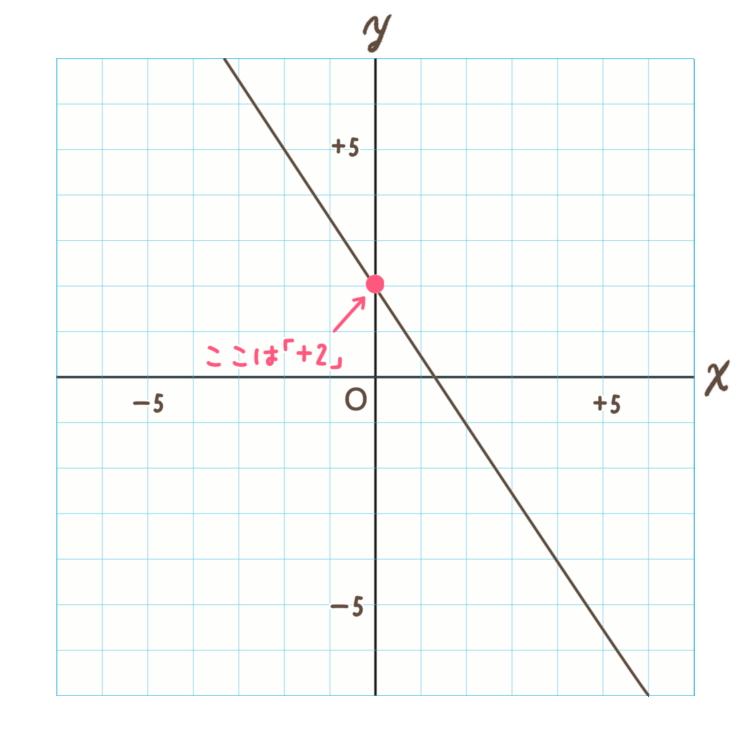
これで切片 \(b\) は「\(+2\)」ということがわかりました。
<手順2>
次に傾き \(a\) を求めます。
グラフのマス目で、縦の線と横の線で、直線と交差している2か所に点をつけます。
1か所は先ほど付けた \(y\) 軸の「\(+2\)」のところで大丈夫です。
もう1か所は、下のグラフで青いところに点をつました。
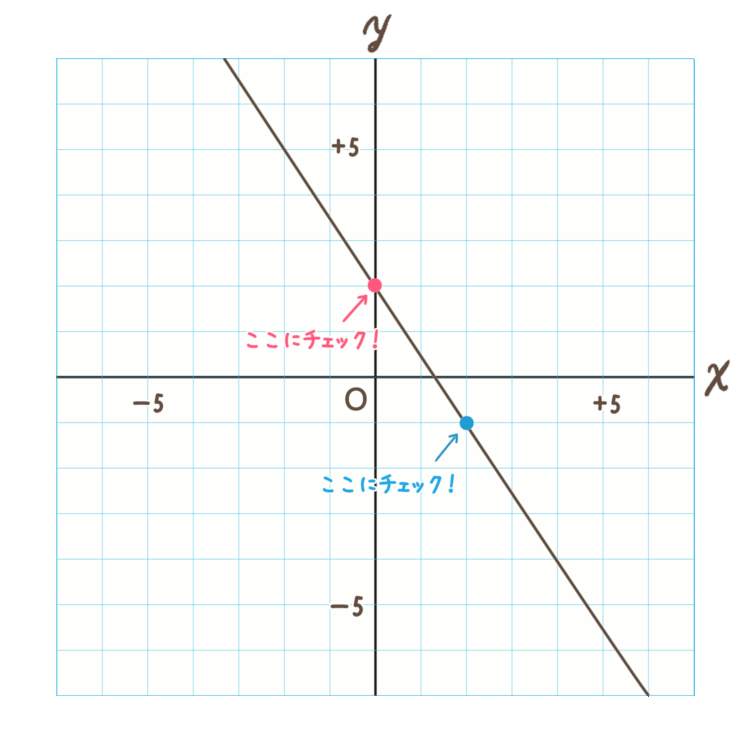
2点にチェックをつけたら、変化の割合を調べます。
下のグラフを見てもらうと、①の点から②の点まで \(x\) が \(2\) 増加、\(y\) が \(-3\) 増加していることがわかりますね。
※ \(y\) が \(-3\)(マイナス\(3\))増加ということは、下向きということです。
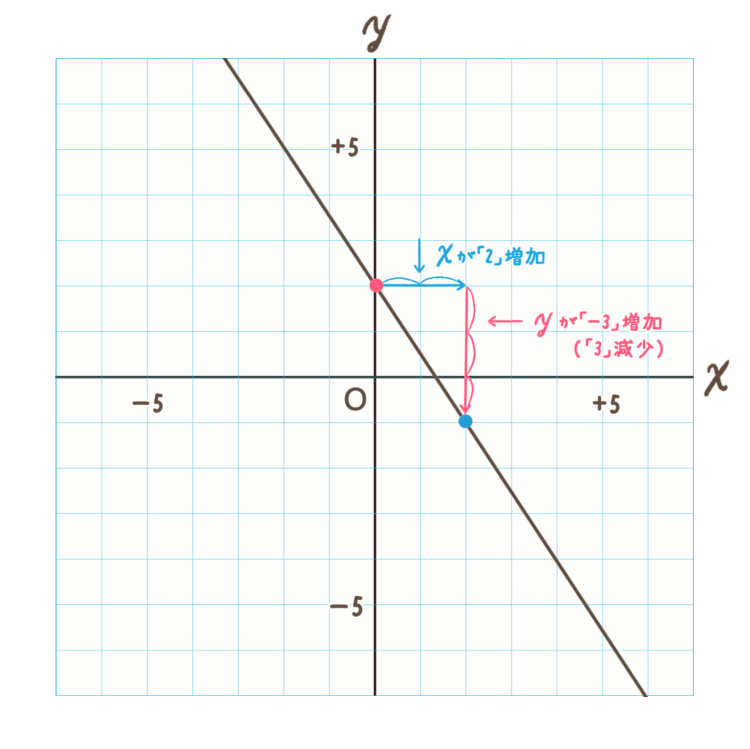
変化の割合は、\(-\frac{3}{2}\) ですね。
一次関数においては、変化の割合=傾きなので、 傾き \(a\) は \(-\)\(\frac{3}{2}\) であるということがわかりました。
<手順3>
基本式 \(y=ax+b\) に求めた \(a\) の値と \(b\) の値を入れます。
\(a\)(傾き)は \(-\frac{3}{2}\) でした。
\(b\)(切片)は \(+2\) でした。
答え. \(y=-\)\(\frac{3}{2}\)\(x+2\)
では練習してみましょう!
問題.
次のグラフの直線の式を求めなさい。
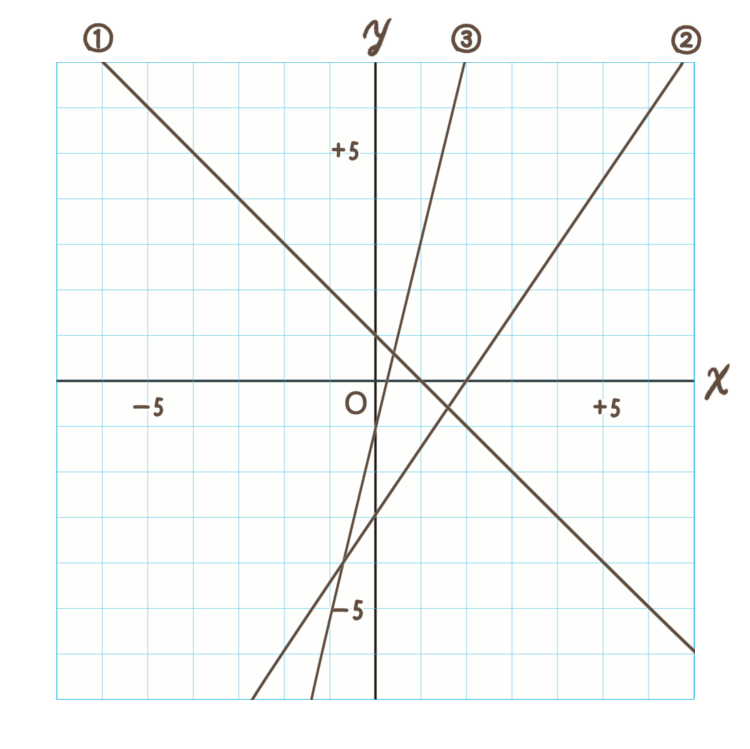
答え
① \(y=-x+1\)
② \(y=\)\(\frac{3}{2}\)\(x-3\)
③ \(y=4x-1\)
グラフの書き取り「直線の式→グラフ」
グラフの読み取り「グラフ→直線の式」
この2パターンは定期テストの鉄板問題ですので、何度も練習して確実にできるようにしていきましょう!
★一次関数★
⑥ 文章→直線の式
グラフの理解が深まりましたら、ここからは“直線の式の求め方”をやっていきます!
ここではグラフを使わずに、文章や数字だけで直線の式を求めます。
いくつかのパターンに分けて紹介していきますね。
<パターン1>
傾きと切片がわかっている場合
これはカンタンです!
初めにも紹介した問題ですがもう一度。
一次関数の基本式「\(y=ax+b\)」の \(a\) に傾き、\(b\) に切片を代入するだけでしたね。
<問題1>
傾きが \(2\)、切片が \(-3\) の一次関数の式を書きなさい
答え. \(y=2x-3\)
<問題2>
傾きが \(-1\)、切片が \(5\) の一次関数の式を書きなさい
答え. \(y=-x+5\)
<パターン2>
傾きと座標がわかっている場合
ここからちょっと難しくなります。
解く手順をしっかり覚えましょう!
<問題1>
傾きが \(3\) で、点(\(1\)、\(4\))を通る直線の式を求めなさい。
傾きが \(3\) ということは、\(y=ax+b\) の \(a\) が \(3\) ですね。
つまり、\(y=\) \(3\)\(x+b\) になります。
点(\(1\)、\(4\))っていうのは、\(x\) が \(1\)、\(y\) が \(4\) っていうことです。
カッコの中に2つの数字があるときは、左の数字が \(x\)、右の数字が \(y\) って覚えておいてください。
先ほどの \(y=3x+b\) の \(x\) に \(1\)、\(y\) に \(4\) を代入して \(b\) の値を求めます。
\(4=3×1+b\)
\(4=3+b\)
\(-b=3-4\)
\(-b=-1\)
\(b=1\)
\(b\) が \(1\) であることがわかりました。
では \(y=3x+b\) の \(b\) に\(1\) を代入します。
答え. \(y=3x+1\)
<問題2>
傾きが \(-4\)、点(\(-2\)、\(5\))を通る直線の式を求めなさい。
\(a=-4\) 、\(x=-2\) 、\(y=5\) を 基本式 \(y=ax+b\) に代入します。
\(5=-4×(-2)+b\)
\(b=-3\)
答え. \(y=-4x-3\)
<問題3>
傾きが \(2\) で、点(\(2\)、\(1\))を通る直線の式を求めなさい。
\(a=2\) 、\(x=2\) 、\(y=1\) を 基本式 \(y=ax+b\) に代入します。
\(1=2×2+b\)
\(b=-3\)
答え. \(y=2x-3\)
<パターン3>
切片と座標がわかっている場合
こいつも<パターン2>と同じ考え方です。
<問題1>
切片が \(2\) で、点(\(1\)、\(4\))を通る直線の式を求めなさい。
\(b=2\) 、\(x=1\) 、\(y=4\) を 基本式 \(y=ax+b\) に代入します。
\(4=a×1+2\)
\(a=2\)
答え. \(y=2x+2\)
<問題2>
切片が \(-5\) で、点(\(-2\)、\(3\))を通る直線の式を求めなさい。
\(b=-5\) 、\(x=-2\) 、\(y=3\) を 基本式 \(y=ax+b\) に代入します。
\(3=a×(-2)-5\)
\(a=-4\)
答え. \(y=-4x-5\)
<パターン4>
2点の座標がわかっている場合
こいつが一番メンドクサイ…
計算の手順も多いので頑張りましょう!!
2点の座標を通る直線の式を求める方法は2つ。
① 変化の割合(傾き)から求める方法
② 連立方程式を使って求める方法
求めるだけならどっちでもいいです!
しかし、定期テストでは解き方を指定される場合もあるので、2つの方法のどちらも出来るようにしてください。
<問題>
グラフが(\(1\)、\(3\))、(\(2\)、\(5\))を通る直線の式を求めなさい。
① 変化の割合(傾き)から求める方法
変化の割合は、\(\frac{yの増加量}{xの増加量}\) でした。
(\(1\)、\(3\))、(\(2\)、\(5\))を通るということは、\(x\) が \(1\) から \(2\) に増加、\(y\) が \(3\) から \(5\) に増加するということです。
増加量はひき算で求められるので、このような式になります。
\(\frac{yの増加量}{xの増加量}\) = \(\frac{5-3}{2-1}\) = \(2\)
これで変化の割合は \(2\) であることがわかりました。
つまり、傾き \(a=2\) ですね。
\(y=ax+b\) の \(a\) に \(2\) を代入します。
\(y=2x+b\)・・・①
次に切片 \(b\) を求めます。
(\(1\)、\(3\))、(\(2\)、\(5\))のどちらが選んでください。
では(\(1\)、\(3\))を選びます。こういうときはカンタンな数字の方を選びましょう。
(\(1\)、\(3\))ということは、\(x\) が \(1\)、\(y\) が \(3\) なので、①の \(x\) と \(y\) にそれぞれを代入します。
\(y=2x+b\)・・・①
↑ \(x\) に \(1\)、 \(y\) に \(3\) を代入
\(3=2×1+b\)
\(b=1\)
傾き \(a\) が \(2\)、切片 \(b\) が \(1\) であることが分かりましたので、基本式の \(a\) と \(b\) に代入し答えを書きます。
答え. \(y=2x+1\)
② 連立方程式を使って求める方法
同じ問題(\(1\)、\(3\))、(\(2\)、\(5\))を通る式を、連立方程式を使って求めます。
カッコに2つの数字があるとき(座標を表すとき)は、左の数字が \(x\) で右の数字が \(y\) でした。ということは・・・
(\(1\)、\(3\))は \(x\) が \(1\)、\(y\) が \(3\) です。
(\(2\)、\(5\))は \(x\) が \(2\)、\(y\) が \(5\)です。
では基本式 \(y=ax+b\) にそれぞれを代入して連立方程式を作ります。
\(3=a+b\)
\(5=2a+b\)
加減法で解いてみましょう!
\(3=a+b\)
\(\underline{-)5=2a+b}\)
\(-2=-a\)
\(a=2\)
\(b\) も求めます。
\(3=a+b\) の \(a\) に \(2\) を代入して \(b\) を求めましょう。
\(3=2+b\)
\(b=1\)
傾き \(a\) が \(2\)、切片 \(b\) が \(1\) であることが分かりましたので、基本式に代入し答えを書きます。
答え. \(y=2x+1\)
いかがでしたか?
2点を通る直線の式は、①変化の割合から求める方法と、②連立方程式を使って求める方法のどちらも同じ答えになりましたね。
計算の手順が少ないのは①ですが、どちらのやり方でも出来るように練習してください。
何問かやってみます!
<問題>
次の2点を通る直線の式を求めなさい。
(1)(\(-2\)、\(9\))、(\(4\)、\(-3\))
(2)(\(2\)、\(-6\))、(\(5\)、\(-9\))
<解説>
(1)(\(-2\)、\(9\))、(\(4\)、\(-3\))
変化の割合から求める方法でやってみます。
\(\frac{-3-9}{4-(-2)}\)=\(\frac{-12}{6}\)=\(-2\)
傾き \(a=-2\)
次に切片 \(b\) を求めます。
(\(4\)、\(-3\))を使います。
\(x=4\)、\(y=-3\) と、さきほど求めた \(a=-2\) を基本式 \(y=ax+b\) に代入します。
\(-3=-2×4+b\)
\(-3=-8+b\)
\(b=5\)
傾き \(a=-2\)、切片 \(b=5\) であることがわかりましたので、基本式 \(y=ax+b\) に代入して答えを書きます。
答え. \(y=-2x+5\)
<解説>
(2)(\(2\)、\(-6\))、(\(5\)、\(-9\))
連立方程式を使って求めてみます。
(\(2\)、\(-6\))は、 \(x\) が \(2\)、\(y\) が \(-6\)
(\(5\)、\(-9\))は、 \(x\) が \(5\)、\(y\) が \(-9\)
それぞれを基本式 \(y=ax+b\) に代入して連立方程式を作ります。
\(-6=2a+b\)
\(-9=5a+b\)
\(-6=2a+b\)
\(\underline{-)-9=5a+b}\)
\(3=-3a\)
\(a=-1\)
\(-6=2a+b\) の式の \(a\) に \(-1\) を代入して \(b\) を求めます。
\(-6=2×(-1)+b\)
\(-6=-2+b\)
\(b=-4\)
傾き \(a=-1\)、切片 \(b=-4\) であることがわかりましたので、基本式 \(y=ax+b\) に代入して答えを書きます。
答え. \(y=-x-4\)
<パターン例外>
〇〇と平行で・・・
これもよく出るパターンです。
「平行」っていう言葉が出たら、傾きが同じって覚えておいてください。
例えば「 \(y=2x+3\) と平行で」と言われたら、傾きが \(2\) ってことです。
切片の \(+3\) は思い切り無視してください!
<問題>
一次関数 \(y=4x-2\) のグラフと平行で、点(\(2\)、\(3\))を通る直線の式を求めなさい。
<解説>
平行ってことは傾きが同じということなので、次の言い方に置き換えられます。
「傾きが \(4\) で、点(\(2\)、\(3\))を通る直線の式を求めなさい」
この時点で、傾き \(a=4\) がわかっています。
これなら先ほど紹介した、
<パターン2>傾きと座標がわかっている場合と同じですね。
基本式 \(y=ax+b\) に、\(a=4\)、\(x=2\)、\(y=3\) を代入し、\(b\) の値を求めます。
\(3=4×2+b\)
\(3=8+b\)
\(b=-5\)
傾き \(a=4\)、切片 \(b=-5\) を基本式に代入して答えを書きます。
答え. \(y=4x-5\)
<パターン例外>
言葉の言いかえ
言葉の言いかえはイジワルな感じですが、意味がちゃんとわかっていればカンタンです!色々やってみましょう!
<問題>
\(x=-3\) のとき \(y=-5\) で、\(x\) の増加量が \(2\) のとき \(y\) の増加量が \(6\) である直線の式を求めなさい。
<解説>
「\(x\) の増加量が \(2\) のとき \(y\) の増加量が \(6\) 」ってことは、傾き \(a\) が \(3\) ということです。
傾き \(a=\) \(\frac{yの増加量=6}{xの増加量=2}\) なので、
\(\frac{6}{2}\) \(=\) \(3\) だから!
傾き \(a\) が \(3\)、\(x\) が \(-3\)、\(y\) が \(-5\) を、基本式 \(y=ax+b\) に代入して \(b\) を求めます。
\(-5=3×(-3)+b\)
\(-5=-9+b\)
\(b=4\)
傾き \(a=3\)、切片 \(b=4\) を基本式に代入して答えを書きます。
答え. \(y=3x+4\)
<問題>
点(\(3\)、\(-1\))を通り、直線 \(y=2x+5\) と \(y\) 軸で交わる直線の式を求めなさい。
<解説>
「\(y\) 軸で交わる」というところがポイントです。
\(y\) 軸と交わるということはそこが切片ということですね。
\(y=2x+5\) と \(y\) 軸で交わるということは、切片が「\(+5\)」ということを言っているんです。
ここでの傾き「\(2\)」は無視してください。
このように変換できますね。
点(\(3\)、\(-1\))を通り、切片が \(5\) の直線の式を求めなさい。
\(x\) が \(3\)、\(y\) が \(-1\)、\(b\)(切片)が \(5\) を基本式 \(y=ax+b\) に代入して、傾き \(a\) を求めます。
\(-1=3a+5\)
\(-3a=5+1\)
\(-3a=6\)
\(a=-2\)
基本式 \(y=ax+b\) に、\(a\) に \(-2\)、\(b\) に \(5\) を代入して答えを書きます。
答え. \(y=-2x+5\)
いかがでしたか?
この辺りから大きく点数を落としてしまう中2生も多いのではないでしょうか?
一次関数では「グラフを書く」「グラフから直線の式を求める」「文章から直線の式を求める」の3パターンは絶対に抑えておきましょう!
定期テストでも高校入試でも必ず出題されるので、何度も問題を解いて確実に自分のモノにしてくださいね!

このページでは、中学2年生の数学で押さえておきたい重要ポイントである“式の計算”、“連立方程式”、“一次関数”について説明させていただきました。
この後に習う、“図形”も証明問題とかが出てくるので超大事です!
冒頭でもお伝えしましたが、数学は思いっきり積み重ねの教科です。
基本があやふやなままだと、あっという間にわからなくなってしまう恐ろしい教科です。
そこに対抗していくには、“基礎の土台”が超重要!
基礎を完璧に理解していけば、あとは練習を重ねることによってどんどん数学が面白くなっていきますよ!
「連立方程式がわからない…」
「一次関数なんて大っキライ!」
そんなお子さんは今すぐ対策をしていかないと、学年が上がるにつれてどんどん勉強が大変になってしまいます。

私たち家庭教師のジャニアスでは、“数学の楽しさ”を教えてたくさんのお子さんに点数アップ、成績アップの結果を出してきました。
今なら!無料の体験授業で勉強のやり方から丁寧に教えていますので、この機会に一度試してみませんか?
もちろん、体験授業を受けていただいたからといって、ご入会への無理な勧誘は一切ありませんのでご安心ください。
体験授業でお会いできることをスタッフ一同、楽しみにしています。

今ご覧になっているページは
数学(中2)です。
▼ よく見られているページ ▼

家庭教師のジャニアスでは下記の地域にお住いの方に家庭教師を紹介しております。下記に含まれていない地域にお住まいのご家庭でも、家庭教師を紹介できる場合もございますので、お気軽にお問い合わせください。

私たちジャニアスは、どんなに効果がある勉強法でもお子さんに合わない・
続けることができなければ「意味がない」と考えています。

塾や家庭教師選びにご苦労されているご家庭も多いと思いますが、ジャニアスの体験授業は、「やる気のきっかけにしたい」「今の塾と比べてみたい」「今すぐは考えてないけど家庭教師がどんなモノかを見てみたい」などのような、気軽な気持ちで受けていただけたらと思います。
もちろん、体験を受けたからといって、無理に入会を勧めるようなことは一切ありませんので、安心してくださいね(^^)











































